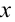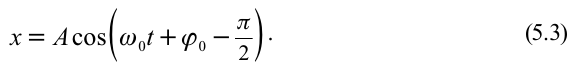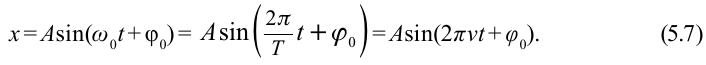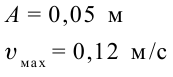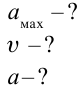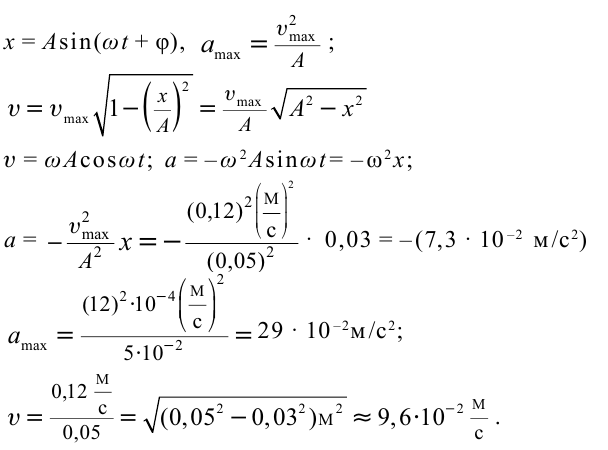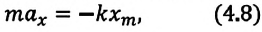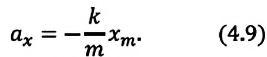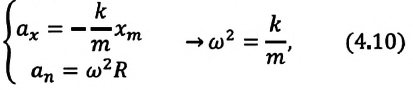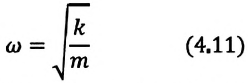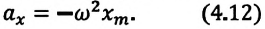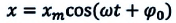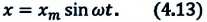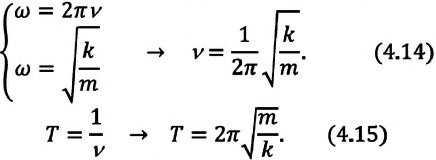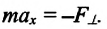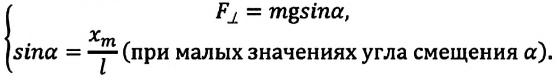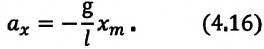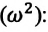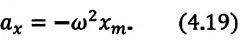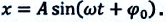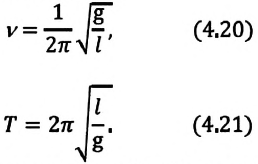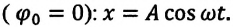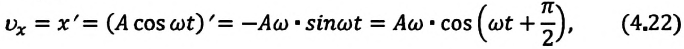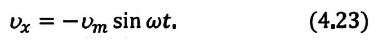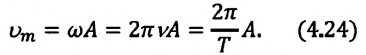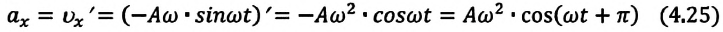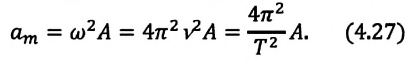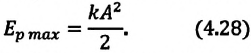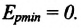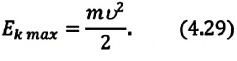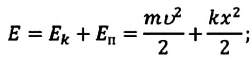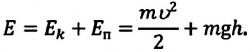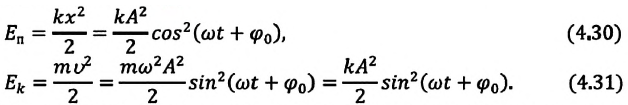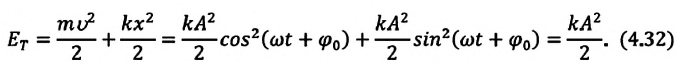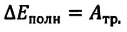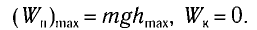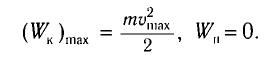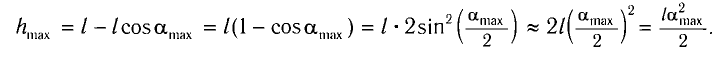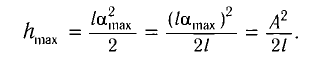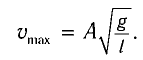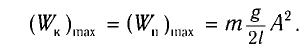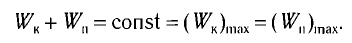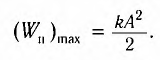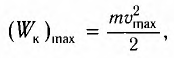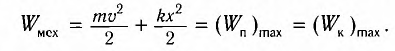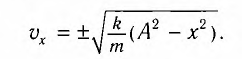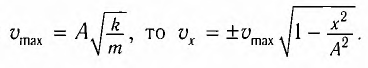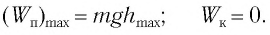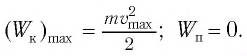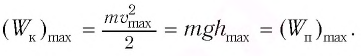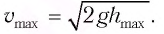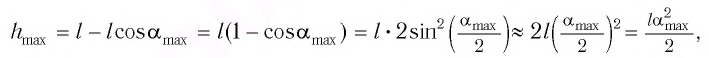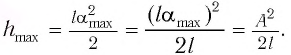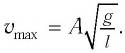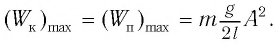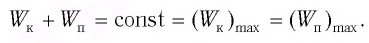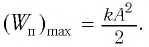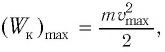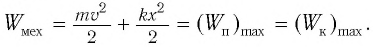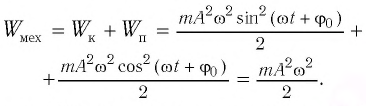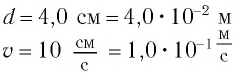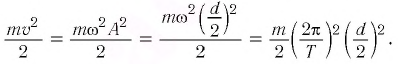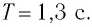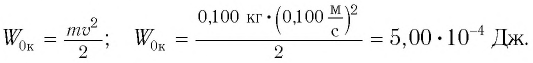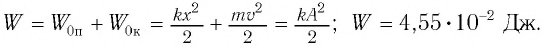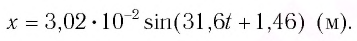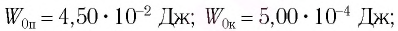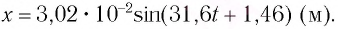Приведите параметры гармонических колебаний чем они определяются

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

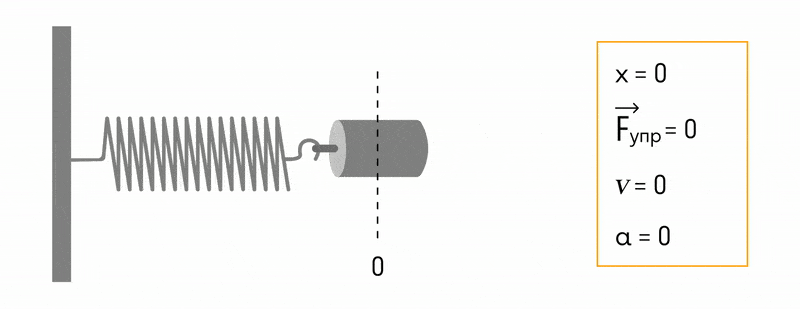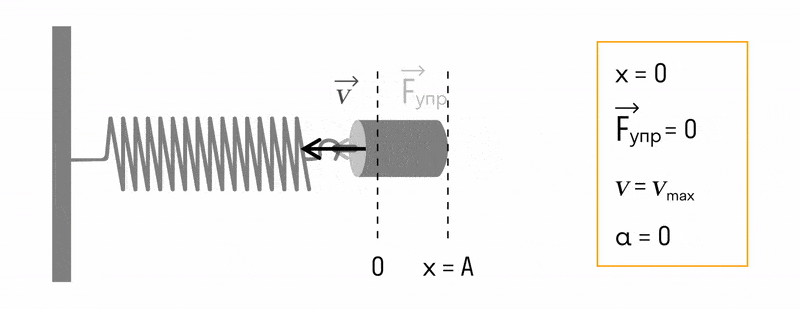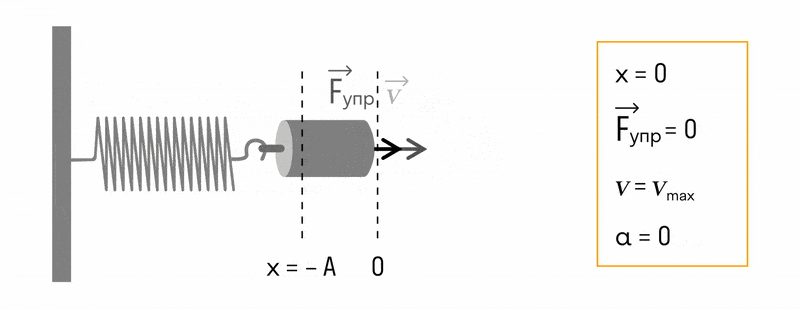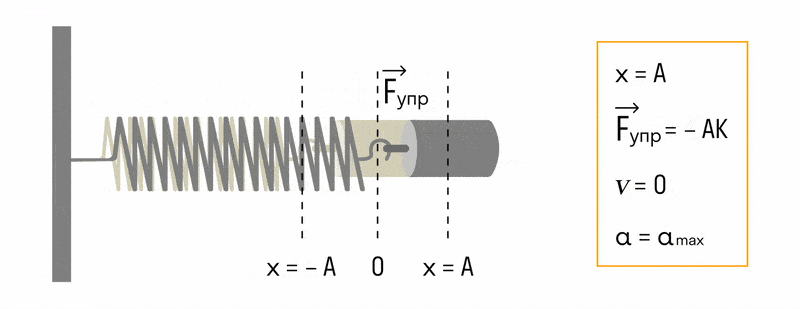
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Источник

Содержание:

Гармонические колебания:

Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.

Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (

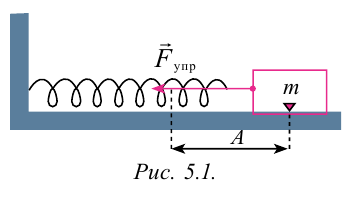
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 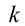, а ее масса ничтожна мала и можно ее не учитывать. Считаем, что масса системы сосредоточена в грузе, а упругость в пружине.

Если груз, который находится в равновесии, потянем вправо на расстояние 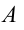и отпустим, то под действием силы упругость, которая появляется в пружине, груз смещается в
сторону равновесного состояния.

С течением времени смещение груза уменьшается относительно , но скорость груза при этом увеличивается. Когда груз доходит до равновесного состояния, его смещение () равняется нулю и соответственно сила упругости равняется нулю. Но груз по инерции начинает двигаться в левую сторону. Модуль силы упругости, которая появляется в пружине, тоже растет. Однако из-за того, что сила упругости постоянно направлена против смещения груза, она начинает тормозить груз. В результате движение груза замедляется, и, в результате, прекращается. Теперь груз под воздействием эластической силы сжатой пружины начинает двигаться в сторону равновесного состояния.
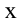
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде ():

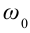
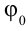
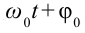
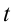
здесь: – циклическая частота, зависящая от параметров колеблющихся систем, – начальная фаза, () фаза колебания с течением времени .
Из математики известно, что 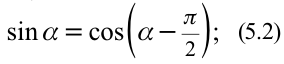поэтому формулу (5.2.) можно записать в виде

Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.

Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.

Основные параметры гармонических колебаний

a) период колебания 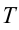– время одного полного колебания:

)

б) частота колебания 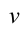– количество колебаний, совершаемых за 1 секунду:

Единица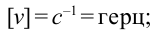
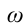
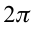
c) циклическая частота – количество колебаний за секунд:

С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.

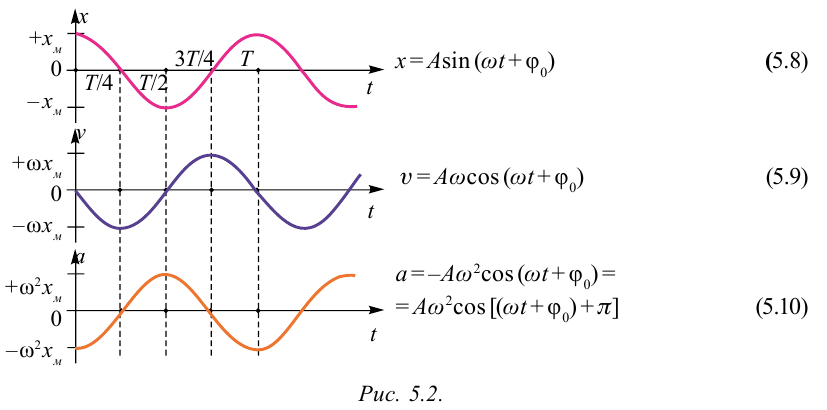
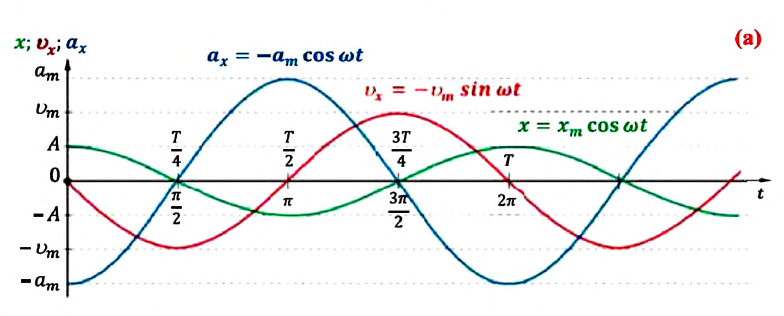
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:

Пример решения задачи:

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

Гармонические колебания пружинного маятника

В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.

Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:

Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.

Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.

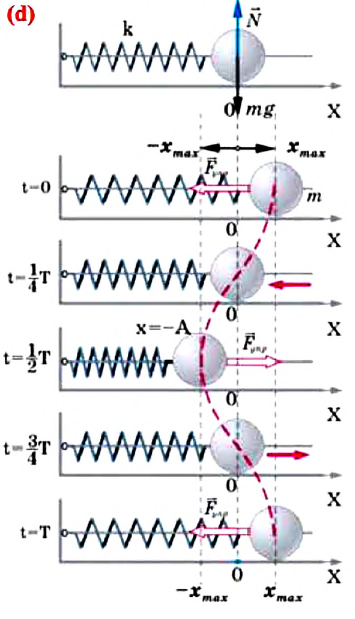
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).

В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 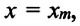сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:

Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.

Таким образом, уравнение движения пружинного маятника можно записать и так:

Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 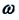являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:

Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.

или

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:

Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.

Гармонические колебания математического маятника

До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.

Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.

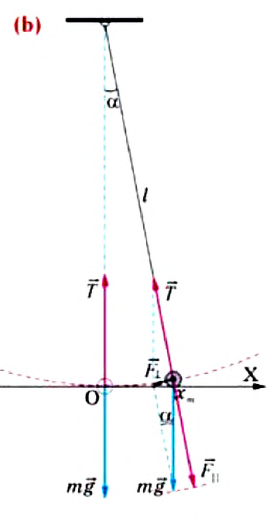
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).

Приняв во внимание, что:

Для уравнения движения математического маятника получим:

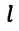
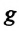
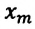
Где — длина математического маятника (нити), — ускорение свободного падения, — амплитуда колебания.

Для данной колебательной системы отношение — постоянная положительная величина, потому что ускорение свободного падения и длина нити не могут быть отрицательными. Если сравнить уравнения (4.16) и (4.10), с легкостью можно увидеть, что отношение также соответствует квадрату циклической частоты

Таким образом, уравнение движения математического маятника можно записать и так:

Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:

Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.

Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:

Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.

Скорость и ускорение при гармонических колебаниях

Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.

При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю

Так как скорость является первой производной смещения (координат) по времени, то:

Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 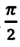(а).

Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:

Так как ускорение является первой производной скорости по времени, то получим:

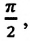
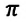
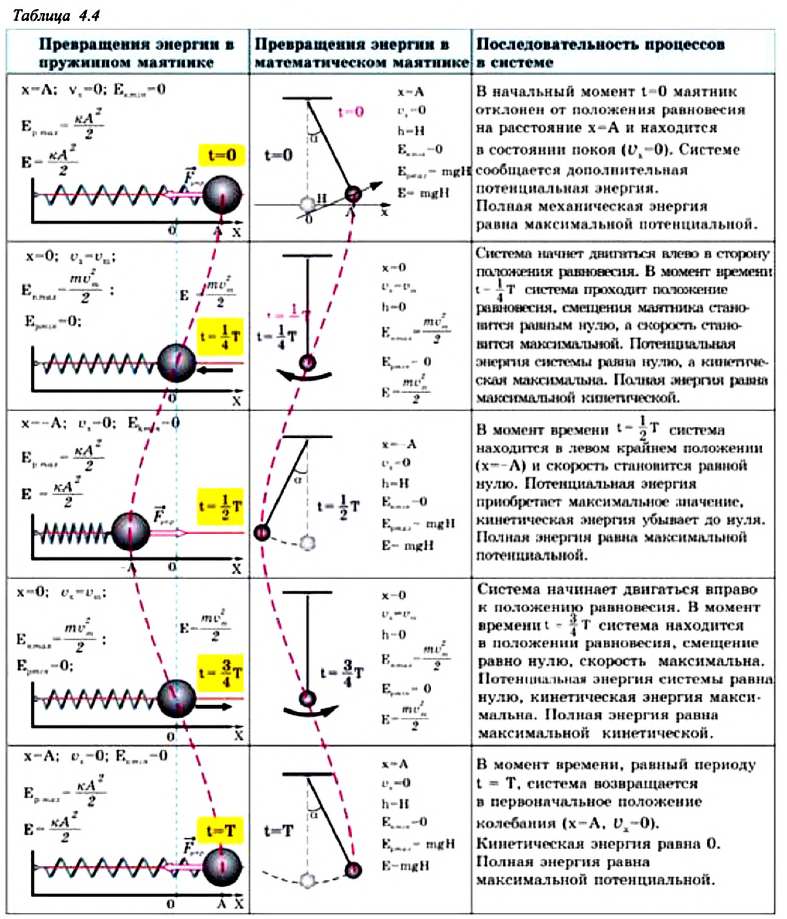
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на а колебания смещения на

(см.: рис. а). Максимальное (амплитудное) значение ускорения зависит от амплитуды, частоты и периода колебаний:

Превращения энергии при гармонических колебаниях

Теоретический материал

Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.

В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 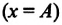имеет максимальное значение:

Если же маятник находится в точке равновесия, потенциальная энергия минимальна:

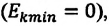
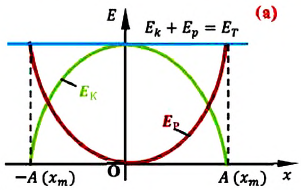
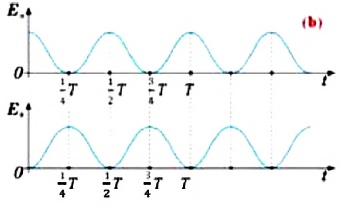
Кинетическая энергия системы, наоборот, в точке возвращения минимальна а в точке равновесия максимальна:

На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.

Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 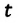остается постоянной (трение не учитывается):

a) для пружинного маятника:

b) для математического маятника:

Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):

Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:

• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.

Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:

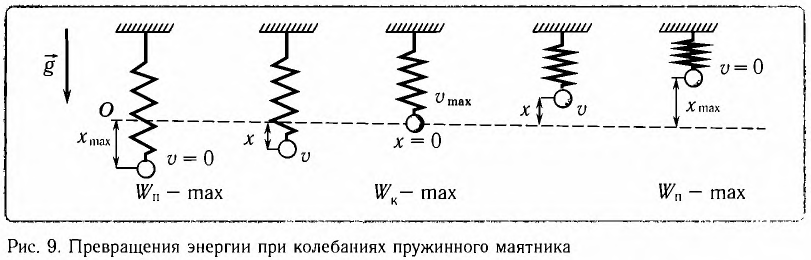
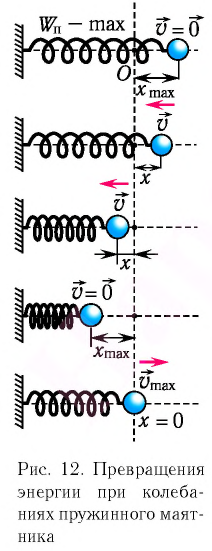
Превращения энергии при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.

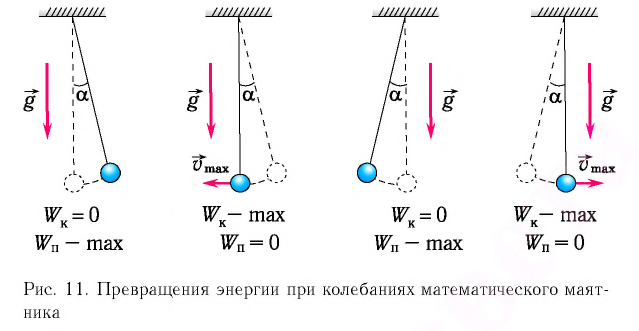
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

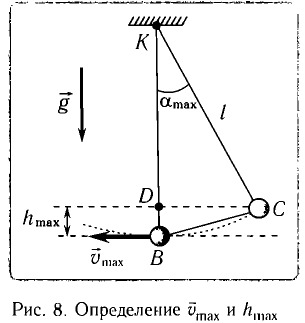
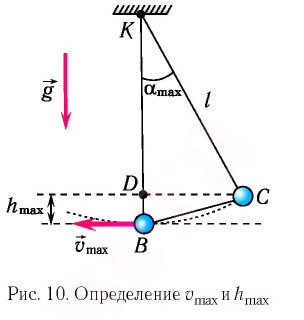
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

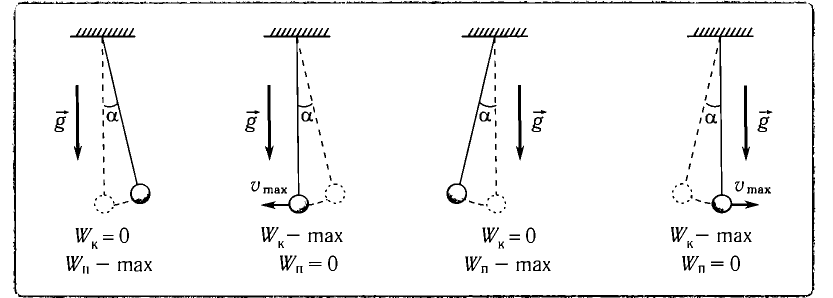
Рис. 7. Превращения энергии при колебаниях математического маятника

Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:

Из закона сохранения механической энергии следует (рис. 8), что

(1)

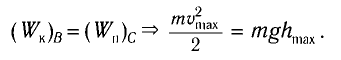
Отсюда найдем модуль максимальной скорости маятника:

(2)

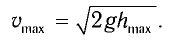
Высоту можно выразить через длину маятника l и амплитуду колебаний А.

Если колебания малые, то 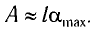Из треугольника KCD на рисунке 8 находим

Подставив выражение для в формулу I (2), получим

Подставляя выражения для 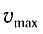и в соотношение (1), находим

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.

В любом промежуточном положении

Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 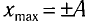, модуль его скорости равен нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:

где 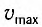— модуль максимальной скорости груза при колебаниях.

В промежуточных точках полная механическая энергия

Отсюда можно вывести выражение для модуля скорости 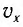груза в точке с

Так как

Энергия при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

При отклонении маятника на угол 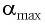(рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

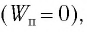
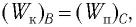
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю то из закона сохранения механической энергии следует (см. рис. 10), что т. е. кинетическая энергия маятника (а следовательно, и скорость) рис. ю. Определение^иhmax будет максимальна:

Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:

Отсюда найдем модуль максимальной скорости маятника:

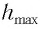
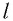
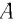
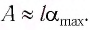
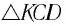
Высоту можно выразить через длину маятника и амплитуду колебаний. Если колебания малые, то Из (см. рис. 10) находим:

или

Подставив выражение (3) для 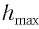в формулу (2), получим:

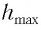
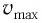
Подставляя выражения (3) для и (4) для в соотношение (1), находим:

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении

Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).

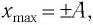
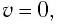
В крайних положениях, когда модуль скорости маятника и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда 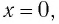вся энергия пружинного маятника переходит в кинетическую энергию груза:

где 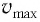— модуль максимальной скорости груза при колебаниях.

В положениях между крайними точками полная энергия

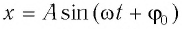
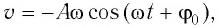
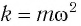
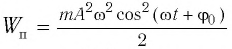
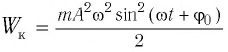
С учетом выражений для координаты и проекции скорости груза а также для находим его потенциальную энергию и кинетическую энергию в произвольный момент времени

Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:

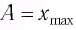
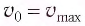
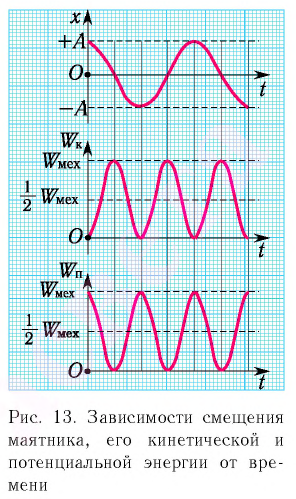
Таким образом, начальное смещение определяет начальную потенциальную, а начальная скорость определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.

Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).

Пример №1

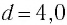
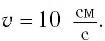
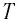
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние см и при прохождении положения равновесия достигает скорости, модуль которой Определите период колебании маятника.
Дано:

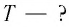
Решение

По закону сохранения механической энергии

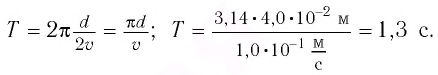
Ответ:

Пример №2

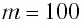
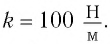
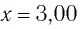
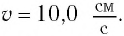
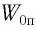
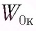
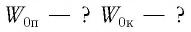
Груз массой г находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью Его смешают на расстояние см от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой Определите потенциальную и кинетическую энергию груза в начальный момент времени. Запишите кинематический закон движения груза.

Решение Потенциальная энергия груза: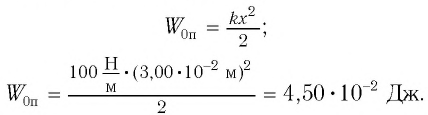

Кинетическая энергия груза:

Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:

Отсюда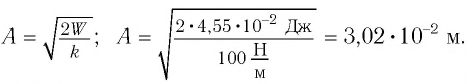

Циклическая частота: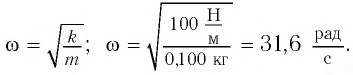

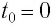
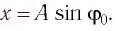
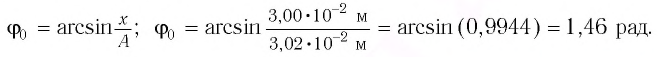
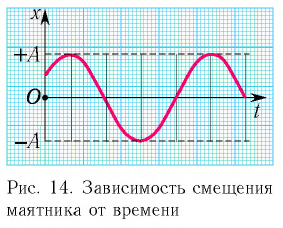
В начальный момент времени координата груза Отсюда начальная фаза:

Тогда закон гармонических колебаний имеет вид (рис. 14):

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

• ← Приведите основные доказательства что корневище это побег
• Приведите по 2 3 примера существительных отвечающих на вопросы кто и что →