при составлении цифрового пятизначного пин кода каждую цифру разрешено использовать не более 3 раз
Математика 8 класс МА2080401 МА2080402 теория вероятностей статград 11 мая 2021
ПОДЕЛИТЬСЯ
Новая тематическая диагностическая работа статград по математике 8 класс по разделу теория вероятностей и статистика ответы и задания для тренировочных вариантов МА2080401, МА2080402. Официальная дата проведения работы 11.05.2021 (11 мая 2021 года).
Ссылка для скачивания вариантов (МА2080401-МА2080402): скачать задания
Ссылка для скачивания всех ответов и критериев: скачать ответы
Диагностическая работа по разделу теория вероятностей и статистика статград по математике 8 класс решать онлайн:
Сложные задания и ответы с вариантов:
1)На основе многолетних наблюдений построена диаграмма количества солнечных дней в нескольких российских городах в течение года. Рассмотрите диаграмму и ответьте на вопросы. а) В каких городах солнечных дней в году меньше, чем в Москве? б) Оцените примерно размах данных ⸻ разницу между наибольшим и наименьшим значениями. в) Медиана значений составляет 177 дней. Найдите медианного представителя в этой выборке городов, то есть город, в котором число солнечных дней наиболее близко к медиане.
2)Монету бросили четыре раза. Найдите вероятность события «орёл выпадет не более одного раза».
3)В городском шахматном турнире участвует 20 игроков из двух шахматных секций, по 10 шахматистов из каждой секции. Игроки распределяются по игровым парам с помощью жребия. Какова вероятность того, что первую партию турнира сыграют шахматисты из разных секций?
4)В таблице собраны данные о доле площади пахотных земель в странах СНГ за 2015 год. Рассмотрите таблицу и ответьте на вопросы. а) Восстановите пропущенное значение: найдите долю пахотных земель в Армении. б) В каких из перечисленных стран пашня составляет больше половины всей территории? в) Средняя площадь пахотных земель в этих странах равна примерно 184,4 тыс. кв. км, а медиана ⸻ 19,7 тыс. кв. км. Чем можно объяснить такое большое отличие между этими двумя показателями?
5)Трое играют в настольную игру. Они по очереди бросают игральный кубик по одному разу, но те из них, у кого выпало 6 очков, получают право на повторный ход. Найдите вероятность того, что ровно двое получат право на повторный ход.
6)При составлении цифрового четырёхзначного пин-кода каждую цифру разрешено использовать не более двух раз. Например, коды 0223 и 1327 допускаются, а код 9499 ⸻ не допускается. Сколько существует различных пин-кодов, удовлетворяющих этому условию?
Пракикум «Решение задач по комбинаторике»
Разделы: Математика
Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычный вопрос в комбинаторных задачах: сколькими способами….
К комбинаторным задачам относятся также задачи построения магических квадратов, задачи расшифровки и кодирования.
Рождение комбинаторики как раздела математики связано с трудами великих французских математиков 17 века Блеза Паскаля (1623–1662) и Пьера Ферма (1601–1665) по теории азартных игр. Эти труды содержали принципы определения числа комбинаций элементов конечного множества. С 50-х годов 20 века интерес к комбинаторике возрождается в связи с бурным развитием кибернетики.
Основные правила комбинаторики – это правило суммы и правило произведения.
Если некоторый элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то выбор «либо А, либо В» можно сделать n + m способами.
Например, Если на тарелке лежат 5 яблок и 6 груш, то один плод можно выбрать 5 + 6 = 11 способами.
Если элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то пару А и В можно выбрать n • m способами.
Например, если есть 2 разных конверта и 3 разные марки, то выбрать конверт и марку можно 6 способами (2 • 3 = 6).
Правило произведения верно и в том случае, когда рассматривают элементы нескольких множеств.
Например, если есть 2 разных конверта, 3 разные марки и 4 разные открытки, то выбрать конверт, марку и открытку можно 24 способами (2 • 3 • 4 = 24).
Произведение всех натуральных чисел от 1 до n включительно называется n – факториалом и обозначается символом n!
Например, 5! = 1 • 2 • 3 • 4 • 5 = 120.
Принято считать 0! равным 1.
Число перестановок из n равна n!
Например, если есть 3 шарика – красный, синий и зелёный, то выложить их в ряд можно 6 способами (3 • 2 • 1 = 3! = 6).
Иногда комбинаторная задача решается с помощью построения дерева возможных вариантов.
Например, решим предыдущую задачу о 3-х шарах построением дерева.
Практикум по решению задач по комбинаторике.
1. В вазе 6 яблок, 5 груш и 4 сливы. Сколько вариантов выбора одного плода?
2. Сколько существует вариантов покупки одной розы, если продают 3 алые, 2 алые и 4 жёлтые розы?
3. Из города А в город В ведут пять дорог, а из города В в город С ведут три дороги. Сколько путей, проходящих через В, ведут из А в С?
4. Сколькими способами можно составить пару из одной гласной и одной согласной букв слова «платок»?
гласные: а, о – 2 шт.
согласные: п, л, т, к – 4 шт.
5. Сколько танцевальных пар можно составить из 8 юношей и 6 девушек?
6. В столовой есть 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать?
Ответ: 28 вариантов.
7. Сколько различных двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 3 способа
3 цифра – 3 способа
Ответ: 9 различных двузначных чисел.
8. Сколько различных трёхзначных чисел можно составить, используя цифры 3 и 5, если цифры могут повторяться?
1 цифра – 2 способа
2 цифра – 2 способа
3 цифра – 2 способа
Ответ: 8 различных чисел.
9. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 4 способа
Ответ: 12 различных чисел.
10. Сколько существует трёхзначных чисел, у которых все цифры чётные?
1 цифра – 4 способа
2 цифра – 5 способов
3 цифра – 5 способов
Ответ: существует 100 чисел.
11. Сколько существует четных трёхзначных чисел?
1 цифра – 9 способов (1, 2, 3, 4, 5, 6, 7, 8, 9)
2 цифра – 10 способов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
3 цифра – 5 способов (0, 2, 4, 6, 8)
Ответ: существует 450 чисел.
12.Сколько различных трёхзначных чисел можно составить из трёх различных цифр 4, 5, 6?
1 цифра – 3 способа
2 цифра – 2 способа
3 цифра – 1 способ
Ответ: 6 различных чисел.
13. Сколькими способами можно обозначить вершины треугольника, используя буквы А, В, С, D?
1 вершина – 4 способа
2 вершина – 3 способа
3 вершина – 2 способа
14. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5,при условии, что ни одна цифра не повторяется?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа
Ответ: 60 различных чисел.
15. Сколько различных трёхзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая из этих цифр может быть использована только один раз?
1 цифра – 2 способа
2 цифра – 4 способа
3 цифра – 3 способа
Ответ: 24 различных числа.
16. Сколькими способами можно составить флаг, состоящий из трёх горизонтальных полос различных цветов, если имеется материал шести цветов?
1 полоса – 6 способов
2 полоса – 5 способов
3 полоса – 4 способа
17. Из класса выбирают 8 человек, имеющих лучшие результаты по бегу. Сколькими способами можно составить из них команду из трёх человек для участия в эстафете?
1 человек – 8 способов
2 человек – 7 способов
3 человек – 6 способов
18. В четверг в первом классе должно быть четыре урока: письмо, чтение, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
1 урок – 4 способа
2 урок – 3 способа
3 урок – 2 способа
4 урок – 1 способ
19. В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все уроки разные?
1 урок – 8 вариантов
2 урок – 7 вариантов
3 урок – 6 вариантов
4 урок – 5 вариантов
5 урок – 4 варианта
8 • 7 • 6 • 5 • 4 = 6720
20. Шифр для сейфа составляется из пяти различных цифр. Сколько различных вариантов составления шифра?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа
4 цифра – 2 способа
5 цифра – 1 способ
5 • 4 • 3 • 2 • 1 = 120
21. Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов?
22. Сколько вариантов семизначных телефонных номеров можно составить, если исключить из них номера, начинающиеся с нуля и 9?
1 цифра – 8 способов
2 цифра – 10 способов
3 цифра – 10 способов
4 цифра – 10 способов
5 цифра – 10 способов
6 цифра – 10 способов
7 цифра – 10 способов
8 • 10 • 10 • 10 • 10 • 10 • 10 = 8.000.000
23. Телефонная станция обслуживает абонентов, у которых номера телефонов состоят из 7 цифр и начинаются с 394. На сколько абонентов рассчитана эта станция?
№ телефона 394
10 • 10 • 10 • 10 = 10.000
24. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были различных размеров?
Левые перчатки – 6 способов
Правые перчатки – 5 способов (6 перчатка того же размера, что и левая)
5 цифра – 2 способа (две чётные цифры)
4 цифра – 4 способа
3 цифра – 3 способа
2 цифра – 2 способа
1 цифра – 1 способ
26. Сколько существует четырёхзначных чисел, составленных из нечётных цифр и делящихся на 5?
Нечётные цифр – 1, 3, 5, 7, 9.
Из них делятся на 5 – 5.
4 цифра – 1 способ (цифра 5)
3 цифра – 4 способа
2 цифра – 3 способа
1 цифра – 2 способа
27. Сколько существует пятизначных чисел, у которых третья цифра – 7, последняя цифра – чётная?
1 цифра – 9 способов (все, кроме 0)
2 цифра – 10 способов
3 цифра – 1 способ (цифра 7)
4 цифра – 10 способов
5 цифра – 5 способов (0, 2, 4, 6, 8)
9 • 10 • 1 • 10 • 5 = 4500
28. Сколько существует шестизначных чисел, у которых вторая цифра – 2, четвёртая – 4, шестая – 6, а все остальные – нечётные?
1 цифра – 5 вариантов (из 1, 3, 5, 7, 9)
2 цифра – 1 вариант (цифра 2)
3 цифра – 5 вариантов
4 цифра – 1 вариант (цифра 4)
5 цифра – 5 вариантов
6 цифра – 1 вариант (цифра 6)
5 • 1 • 5 • 1 • 5 • 1 = 125
29.Сколько различных чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
Однозначных – 2
Двузначных – 2 • 2 = 4
Трёхзначных – 2 • 2 • 2 = 8
Четырёхзначных – 2 • 2 • 2 • 2 =16
Пятизначных – 2 • 2 • 2 • 2 • 2 = 32
Шестизначных – 2 • 2 • 2 • 2 2 • 2 = 64
Всего: 2 + 4 + 8 + 16 + 32 + 64 = 126
30. В футбольной команде 11 человек. Нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Капитан – 11 способов
Заместитель – 10 способов
31.В классе учатся 30 человек. Сколькими способами из них можно выбрать старосту и ответственного за проездные билеты?
Староста – 30 способов
Ответ. за билеты – 29 способов
32. В походе участвуют 12 мальчиков, 10 девочек и 2 учителя. Сколько вариантов групп дежурных из трёх человек (1 мальчик, 1 девочка, 1 учитель) можно составить?
33. Сколько комбинаций из четырёх букв русского алфавита (в алфавите всего 33 буквы) можно составить при условии, что 2 соседние буквы будут разными?
1 буква – 33 способа
2 буква – 32 способа
3 буква – 32 способа
4 буква – 32 способа
Исследование: для безопасности шестизначные PIN-коды не лучше, чем четырехзначные
Немецко-американская команда исследователей с привлечением добровольцев проверила и сравнила безопасность шестизначных и четырёхзначных PIN-кодов для блокировки смартфонов. В случае утери или кражи смартфона лучше быть уверенным хотя бы в том, что информация окажется защищённой от взлома. Так ли это?
Филипп Маркерт из Института ИТ-безопасности Хорста Гёрца Рурского университета Бохума и Максимилиан Голла из Института безопасности и конфиденциальности имени Макса Планка выяснили, что на практике психология довлеет над математикой. С математической точки зрения, надёжность шестизначных PIN-кодов существенно выше, чем четырёхзначных. Но пользователи предпочитают определённые комбинации цифр, поэтому некоторые PIN-коды используются чаще и это почти стирает разницу в сложности между шести- и четырёхзначными кодами.
В исследовании участники экспериментов использовали устройства Apple или Android и устанавливали четырех- или шестизначные PIN-коды. На устройствах Apple с версии iOS 9 появился чёрный список запрещённых цифровых комбинаций для PIN-кодов, выбор которых автоматически запрещён. Исследователи имели на руках как оба чёрных списка (для 6- и 4-значных кодов), так и запускали перебор комбинаций на компьютере. Чёрный список полученных от Apple 4-значных PIN-кодов содержал 274 номера, а 6-значных ― 2910.
Для устройств Apple пользователю даётся 10 попыток ввести PIN-код. По мнению исследователей, в таком случае чёрный список практически не имеет смысла. За 10 попыток оказалось сложно угадать правильный номер, даже если он очень простой (типа 123456). Для устройств Android за 11 часов можно совершить 100 вводов PIN-кода, и в данном случае чёрный список уже является более надёжным средством удержать пользователя от ввода простой комбинации и не допустить взлом смартфона путём перебора номеров.
В эксперименте 1220 участников самостоятельно выбирали PIN-коды, а экспериментаторы пытались угадать их за 10, 30 или 100 попыток. Подбор комбинаций проводился двумя способами. Если включался чёрный список, смартфоны атаковались без использования номеров из списка. Без включённого чёрного списка подбор кода начинался с перебора номеров из чёрного списка (как наиболее часто используемые). В ходе эксперимента выяснилось, что разумно выбранный 4-значный PIN-код при ограничении числа попыток ввода достаточно безопасен и даже немного надёжнее 6-значного.
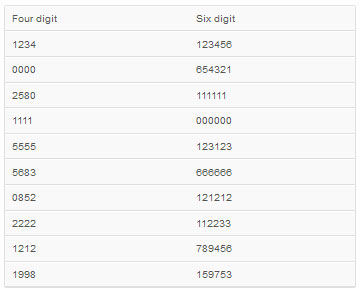
Наиболее распространёнными 4-значными PIN-кодами оказались комбинации 1234, 0000, 1111, 5555 и 2580 (это вертикальный столбец на цифровой клавиатуре). Более глубокий анализ показал, что идеальный черный список для четырехзначных PIN должен содержать около 1000 записей и немного отличаться от того, который был выведен для устройств Apple.
Наиболее часто используемые комбинации PIN-кодов
Наконец, исследователи выяснили, что 4-значные и 6-значные PIN-коды менее безопасны, чем пароли, но более надёжны, чем графическая блокировка смартфонов (по шаблонам). Полный доклад по исследованию будет представлен в Сан-Франциско в мае 2020 года на конференции IEEE Symposium on Security and Privacy.
Информационная безопасность и защита данных (стр. 19 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
Второй метод применения одноразовых паролей для аутентификации пользователей основан на использовании списка случайных паролей, общего для пользователя и проверяющего, и надежного механизма их синхронизации. Разделяемый список одноразовых паролей представляется в виде последовательности или набора секретных паролей, где каждый пароль употребляется только один раз. Данный список должен быть заранее распределен между сторонами аутентификационного обмена. Вариантом данного метода является использование таблицы запросов-ответов, в которой содержатся запросы и ответы, используемые сторонами для проведения аутентификации, причем каждая пара должна применяться только один раз.
Третий метод применения одноразовых паролей для аутентификации пользователей основан на использовании генератора псевдослучайных чисел, общего для пользователя и проверяющего, с одним и тем же начальным значением. Известны следующие варианты реализации этого метода:
— последовательность преобразуемых одноразовых паролей. В ходе очередной сессии аутентификации пользователь создает и передает пароль именно для данной сессии, зашифрованный на секретном ключе, полученном из пароля предыдущей сессии;
— последовательности паролей, основанные на односторонней функции. Суть данного метода составляет последовательное использование односторонней функции (известная схема Лампорта). Этот метод является более предпочтительным с точки зрения безопасности по сравнению с методом последовательно преобразуемых паролей.
Одним из наиболее распространенных протоколов аутентификации на основе одноразовых паролей является стандартизованный в Интернете протокол S/Key (RFC 1760). Данный протокол реализован во многих системах, требующих проверки подлинности удаленных пользователей, в частности в системе TACACS+ компании Cisco.
5.2.3. АУТЕНТИФИКАЦИЯ НА ОСНОВЕ PIN-КОДА
Длина РIN-кода должна быть достаточно большой, чтобы минимизировать вероятность определения правильного PIN-кода методом проб и ошибок. С другой стороны, длина РIN-кода должна быть достаточно короткой, чтобы дать возможность держателям карт запомнить его значение. Согласно рекомендации стандарта ISO 9564-1, PIN-код должен содержать от четырех до двенадцати буквенно-цифровых символов. Однако в большинстве случаев ввод нецифровых символов технически невозможен, поскольку доступна только цифровая клавиатура. Поэтому обычно PIN-код представляет собой четырехразрядное число, каждая цифра которого может принимать значение от 0 до 9.
PIN-код вводится с помощью клавиатуры терминала или компьютера и затем отправляется на смарт-карту. Смарт-карта сравнивает полученное значение PIN-кода с эталонным значением, хранимым в карте, и отправляет результат сравнения на терминал. Ввод PIN-кода относится к мерам безопасности, особенно для финансовых транзакций, и следовательно, требования к клавиатуре часто определяются в этой прикладной области. PIN-клавиатуры имеют все признаки модуля безопасности, и они шифруют PIN-код сразу при его вводе. Это обеспечивает надежную защиту против проникновения в клавиатуру для того, чтобы перехватить PIN-код в то время, когда он вводится.
Различают статические и изменяемые PIN-коды. Статический PIN-код не может быть изменен пользователем, поэтому пользователь должен надежно его хранить. Если он станет известен постороннему, пользователь должен уничтожить карту и получить новую карту с другим фиксированным PIN-кодом.
Изменяемый PIN-код может быть изменен согласно пожеланиям пользователя или заменен на число, которое пользователю легче запомнить. Однако при таком подходе возникает опасность быстрого раскрытия подобного PIN-кода, поскольку числа, которые большинство людей считают удобными для запоминания, являются тривиальными числами вида 1234, 4321, 5115 и т. п. Смарт-карта обычно не проверяет употребление таких тривиальных чисел, поскольку для хранения необходимой таблицы не хватает доступной памяти. Однако терминал может воспрепятствовать замене PIN на такое число.
Некоторые приложения используют также транспортные PIN-коды. Смарт-карта персонализируется со случайным значением PIN-кода, и держатель карты получает значение PIN-кода в заказном письме. Однако, начиная применять карту, пользователь должен заменить PIN-код, использованный при персонализации карты, на выбранный им самим. Такая процедура исключает возможность того, что PIN-код, выслеженный во время персонализации, позже может быть незаконно использован.
Вероятность угадывания PIN-кода. Простейшей атакой на PIN-код, помимо подглядывания через плечо за вводом его с клавиатуры, является угадывание его значения. Вероятность угадывания зависит от длины угадываемого PIN-кода, от составляющих его символов и от количества разрешенных попыток ввода.
Для оценки риска, связанного с использованием конкретного PIN-кода, могут быть использованы формулы вычисления вероятности угадывания.
Тогда число возможных комбинаций PIN-кода определяется формулой
Вероятность угадывания PIN-кода за і попыток определяется формулой
Если РIN-код состоит из четырех десятичных цифр, то есть n = 4 и m = 10, тогда число возможных комбинаций PIN-кода равно х = mn = 104 =, то есть злоумышленник, пытающийся угадать значение PIN-кода, оказывается перед проблемой выбора одной из десяти тысяч комбинаций.
Если число разрешенных попыток ввода і = 3, тогда вероятность угадывания правильного значения PIN-кода из четырех десятичных цифр за три попытки ввода составляет 
или 0,03%.
Спецификации PC/SC рекомендуют, чтобы в смарт-картах были установлены ограничения на число неверных попыток ввода PIN-кода. Когда число обнаруженных неверных попыток достигает заданного предела, процесс ввода должен быть заблокирован, препятствуя дальнейшим попыткам аутентификации. Рекомендуется устанавливать допускаемое число неверных попыток в диапазоне от 1 до 255. Метод, используемый для разблокирования процесса ввода, должен быть защищен независимым механизмом аутентификации.
Генерация PIN-кода. Для генерации PIN-кода смарт-карты используются генератор случайных чисел и алгоритм, который преобразует случайное число в PIN-код необходимой длины. Затем можно использовать таблицу известных тривиальных комбинаций, чтобы распознать и отбросить значение PIN-кода, совпадающее с одной из таких комбинаций. Наконец этот PIN-код записывается в смарт-карту в виде соответствующей криптограммы. Вычисленное значение РIN-кода передается также держателю смарт-карты через защищенный канал.
В настоящее время все дебетовые карты (такие, как карты Eurocheque) из соображений совместимости имеют магнитные полосы, даже если они оснащены микроконтроллерами. Для гибридных карт с чипом и магнитной полосой генерация PIN-кода несколько усложняется. Это обусловлено тем, что банкомат или кассир-автомат, работающий в автономном режиме, должен иметь возможность проверить введенный PIN-код, основанный на данных, расположенных на магнитной полосе. Поэтому алгоритм генерации PIN-кода для гибридных карт с чипом и магнитной полосой должен быть детерминированным, то есть он должен всегда выдавать один и тот же результат для заданного набора входных величин. Генератор случайных чисел не позволяет это сделать. Соответственно, нужна процедура, которая может генерировать PIN-код, основанный на данных магнитной полосы. Чтобы избежать зависимости безопасности системы от самой процедуры генерации PIN-кода, в процесс вычисления должен быть также включен секретный ключ.
Схема алгоритма генерации PIN-кода с использованием симметричного шифра с секретным ключом показана на рис. 5.3.
Этот алгоритм генерирует четырехразрядный PIN-код. Входами алгоритма генерации являются три связанных с картой элемента данных (номер счета, порядковый номер карты, код банка). Над этими данными выполняются операции сцепления, усечения и преобразования в двоично-десятичную форму. Затем выполняется шифрование с использованием симметричного шифра 3-DЕS с секретным ключом. После выполнения процесса шифрования, выделяются четыре шестнадцатеричных символа и выполняется преобразование шестнадцатеричного числа в десятичное.
Главное требование безопасности использования PIN-кода состоит в том, что значение PIN-кода должно запоминаться держателем карты и его нельзя хранить в любой читаемой форме. Но память людей несовершенна, и часто они забывают значения своих PIN-кодов. Поэтому эмитенты карт должны иметь специальные процедуры для таких случаев. Эмитент может реализовать один из следующих подходов. Первый основан на восстановлении забытого клиентом значения PIN-кода и отправке его обратно владельцу карты. При втором подходе просто генерируется новое значение PIN-кода.
При идентификации клиента по значению PIN-кода и предъявленной карте используется два основных способа проверки PIN-кода: неалгоритмический и алгоритмический.
Неалгоритмический способ проверки PIN-кода не требует применения специальных алгоритмов. Проверка PIN-кода осуществляется путем непосредственного сравнения введенного клиентом PIN-кода со значениями, хранимыми в базе данных. Обычно база данных со значениями PIN-кодов клиентов шифруется методом прозрачного шифрования, чтобы повысить ее защищенность, не усложняя процесса сравнения.
Алгоритмический способ проверки PIN-кода заключается в том, что введенный клиентом PIN-код преобразуют по определенному алгоритму с использованием секретного ключа и затем сравнивают со значением PIN-кода, хранящимся в определенной форме на карте. Достоинства этого метода проверки:
— отсутствие копии PIN-кода на главном компьютере исключает его раскрытие обслуживающим персоналом;
— отсутствие передачи PIN-кода между банкоматом или кассиром-автоматом и главным компьютером банка исключает его перехват злоумышленником или навязывание результатов сравнения;
— упрощение работы по созданию программного обеспечения системы, так как уже нет необходимости действий в реальном масштабе времени.
5.3. СТРОГАЯ АУТЕНТИФИКАЦИЯ
Идея строгой аутентификации, реализуемая в криптографических протоколах, заключается в следующем. Проверяемая (доказывающая) сторона доказывает свою подлинность проверяющей стороне, демонстрируя знание некоторого секрета. Например, этот секрет может быть предварительно распределен безопасным способом между сторонами аутентификационного обмена. Доказательство знания секрета осуществляется с помощью последовательности запросов и ответов с использованием криптографических методов и средств.
Существенным является тот факт, что доказывающая сторона демонстрирует только знание секрета, но сам секрет в ходе аутентификационного обмена не раскрывается. Это обеспечивается посредством ответов доказывающей стороны на различные запросы проверяющей стороны. При этом результирующий запрос зависит только от пользовательского секрета и начального запроса, который обычно представляет произвольно выбранное в начале протокола большое число.
В большинстве случаев строгая аутентификация заключается в том, что каждый пользователь аутентифицируется по признаку владения своим секретным ключом. Иначе говоря, пользователь имеет возможность определить, владеет ли его партнер по связи надлежащим секретным ключом и может ли он использовать этот ключ для подтверждения того, что он действительно является подлинным партнером по информационному обмену.
В соответствии с рекомендациями стандарта Х.509 различают процедуры строгой аутентификации следующих типов:
Односторонняя аутентификация предусматривает обмен информацией только в одном направлении. Данный тип аутентификации позволяет:
— подтвердить подлинность только одной стороны информационного обмена;
— обнаружить нарушение целостности передаваемой информации;
— обнаружить проведение атаки типа «повтор передачи»;
— гарантировать, что передаваемыми аутентификационными данными может воспользоваться только проверяющая сторона;
Двусторонняя аутентификация по сравнению с односторонней содержит дополнительный ответ проверяющей стороны доказывающей стороне, который должен убедить ее, что связь устанавливается именно с той стороной, которой были предназначены аутентификационные данные.
Трехсторонняя аутентификация содержит дополнительную передачу данных от доказывающей стороны проверяющей. Этот подход позволяет отказаться от использования меток времени при проведении аутентификации.
Следует отметить, что данная классификация достаточно условна. Отмеченные особенности носят в большей степени теоретический характер. На практике набор используемых приемов и средств зависит непосредственно от конкретных условий реализации процесса аутентификации. Необходимо также учитывать, что проведение строгой аутентификации требует обязательного согласования сторонами используемых криптографических алгоритмов и ряда дополнительных параметров.
Прежде чем перейти к рассмотрению конкретных вариантов протоколов строгой аутентификации, следует остановиться на назначении и возможностях так называемых одноразовых параметров, используемых в протоколах аутентификации. Эти одноразовые параметры иногда называют nonces. По определению, nonce – это величина, используемая для одной и той же цели не более одного раза.
Среди используемых на сегодняшний день одноразовых параметров следует выделить случайные числа, метки времени и номера последовательностей.
Одноразовые параметры позволяют избежать повтора передачи, подмены стороны аутентификационного обмена и атаки с выбором открытого текста. При помощи одноразовых параметров можно обеспечить уникальность, однозначность и временные гарантии передаваемых сообщений. Различные типы одноразовых параметров могут употребляться как отдельно, так и дополнять друг друга.
Можно привести следующие примеры применения одноразовых параметров:
— обеспечение своевременности или гарантий уникальности. Осуществляется путем непосредственного контроля одноразовых параметров протокола (посредством выбора случайного числа) либо косвенно (путем анализа информации, содержащейся в разделяемом секрете);
— однозначная идентификация сообщения или последовательности сообщений. Осуществляется посредством выработки одноразового значения из монотонно возрастающей последовательности (например, последовательности серийных номеров или меток времени) или случайных чисел соответствующей длины.
Следует отметить, что одноразовые параметры широко используются и в других вариантах криптографических протоколов (например, в протоколах распределения ключевой информации).
В зависимости от используемых криптографических алгоритмов протоколы строгой аутентификации можно разделить на следующие группы:
— протоколы строгой аутентификации на основе симметричных алгоритмов шифрования;
— протоколы строгой аутентификации на основе однонаправленных ключевых хэш-функций;
— протоколы строгой аутентификации на основе асимметричных алгоритмов шифрования;
— протоколы строгой аутентификации на основе алгоритмов электронной цифровой подписи.
5.3.1. СТРОГАЯ АУТЕНТИФИКАЦИЯ, ОСНОВАННАЯ НА СИММЕТРИЧНЫХ АЛГОРИТМАХ
Для работы протоколов аутентификации, построенных на основе симметричных алгоритмов, необходимо, чтобы проверяющий и доказывающий с самого начала имели один и тот же секретный ключ. Для закрытых систем с небольшим количеством пользователей каждая пара пользователей может заранее разделить его между собой. В больших распределенных системах, применяющих технологию симметричного шифрования, часто используются протоколы аутентификации с участием доверенного сервера, с которым каждая сторона разделяет знание ключа. Такой сервер распределяет сеансовые ключи для каждой пары пользователей всякий раз, когда один из них запрашивает аутентификацию другого. Кажущаяся простота данного подхода является обманчивой, на самом деле разработка протоколов аутентификации этого типа является сложной и с точки зрения безопасности неочевидной.
Протоколы аутентификации с симметричными алгоритмами шифрования
Ниже приводится три примера отдельных протоколов аутентификации, специфицированных в ISO/IEC 9798-2. Эти протоколы предполагают предварительное распределение разделяемых секретных ключей. Рассмотрим следующие варианты аутентификации:
— односторонняя аутентификация с использованием меток времени;
— односторонняя аутентификация с использованием случайных чисел;
В каждом из этих случаев пользователь доказывает свою подлинность, демонстрируя знание секретного ключа, так как производит дешифрование запросов с помощью этого секретного ключа.
При использовании в процессе аутентификации симметричного шифрования необходимо также реализовать механизмы обеспечения целостности передаваемых данных на основе общепринятых способов.
Введем следующие обозначения:
rA – случайное число, сгенерированное участником А;
rB – случайное число, сгенерированное участником В;
tA – метка времени, сгенерированная участником А;
EK – симметричное шифрование на ключе К (ключ К должен быть предварительно распределен между А и В).
1) Односторонняя аутентификация, основанная на метках времени: 
После получения и дешифрования данного сообщения участник В убеждается в том, что метка времени tA действительна и идентификатор В, указанный в сообщении, совпадает с его собственным. Предотвращение повторной передачи данного сообщения основывается на том, что без знания ключа невозможно изменить метку времени tA и идентификатор В.
2) Односторонняя аутентификация, основанная на использовании случайных чисел:
Участник В отправляет участнику А случайное число rB. Участник А шифрует сообщение, состоящее из полученного числа rB и идентификатора В, и отправляет зашифрованное сообщение участнику В. Участник В расшифровывает полученное сообщение и сравнивает случайное число, содержащееся в сообщении, с тем, которое он послал участнику А. Дополнительно он проверяет имя, указанное в сообщении.
3) Двусторонняя аутентификация, использующая случайные значения:
При получении второго сообщения участник В выполняет те же проверки, что и в предыдущем протоколе, и дополнительно расшифровывает случайное число rА для включения его в третье сообщение для участника А. Третье сообщение, полученное участником А, позволяет ему убедиться на основе проверки значений rA и rB, что он имеет дело именно с участником В.
Широко известными представителями протоколов, обеспечивающих аутентификацию пользователей с привлечением в процессе аутентификации третьей стороны, являются протокол распределения секретных ключей Нидхэма и Шредера и протокол Kerberos.
Протоколы, основанные на использовании однонаправленных ключевых хэш-функций
Протоколы, представленные выше, могут быть модифицированы путем замены симметричного шифрования на шифрование с помощью односторонней ключевой хэш-функции. Это бывает необходимо, если алгоритмы блочного шифрования недоступны или не отвечают предъявляемым требованиям (например, в случае экспортных ограничений).
Своеобразие шифрования с помощью односторонней хэш-функции заключается в том, что оно, по существу, является односторонним, то есть не сопровождается обратным преобразованием – дешифрованием на принимающей стороне. Обе стороны (отправитель и получатель) используют одну и ту же процедуру одностороннего шифрования.
Односторонняя хэш-функция hK(·) с параметром-ключом К, примененная к шифруемым данным M, дает в результате хэш-значение m (дайджест), состоящее из фиксированного небольшого числа байтов (рис. 5.4).
Дайджест m = hK(М) передается получателю вместе с исходным сообщением M. Получатель сообщения, зная, какая односторонняя хэш-функция была применена для получения дайджеста, заново вычисляет ее, используя расшифрованное сообщение M. Если значения полученного дайджеста m и вычисленного дайджеста m’ совпадают, значит, содержимое сообщения М не было подвергнуто никаким изменениям.
Знание дайджеста не дает возможности восстановить исходное сообщение, но позволяет проверить целостность данных. Дайджест можно рассматривать как своего рода контрольную сумму для исходного сообщения. Однако между дайджестом и обычной контрольной суммой имеется и существенное различие. Контрольную сумму используют как средство проверки целостности передаваемых сообщений по ненадежным линиям связи. Это средство проверки не рассчитано на борьбу со злоумышленниками, которым в такой ситуации ничто не мешает подменить сообщение, добавив к нему новое значение контрольной суммы, Получатель в таком случае не заметит никакой подмены.
В отличие от обычной контрольной суммы, при вычислении дайджеста применяются секретные ключи. В случае если для получения дайджеста используется односторонняя хэш-функция с параметром-ключом K, который известен только отправителю и получателю, любая модификация исходного сообщения будет немедленно обнаружена.
На рис. 5.5 показан другой вариант использования односторонней хэш-функции для проверки целостности данных. В этом случае односторонняя хэш-функция h() не имеет параметра-ключа, но зато применяется не просто к сообщению М, а к сообщению, дополненному секретным ключом K, то есть отправитель вычисляет дайджест 
. Получатель, извлекая исходное сообщение M, также дополняет его тем же известным ему секретным ключом K, после чего применяет к полученным данным одностороннюю хэш-функцию h(.). Результат вычислений – 
дайджест m’, который сравнивается с полученным по сети дайджестом m.
При использовании для аутентификации односторонних функций шифрования в рассмотренные выше протоколы необходимо внести следующие изменения:
— функция симметричного шифрования Еk заменяется функцией hk;
— проверяющий, вместо установления факта совпадения полей в расшифрованных сообщениях с предполагаемыми значениями, вычисляет значение однонаправленной функции и сравнивает его с полученным от другого участника обмена информацией;
— для обеспечения возможности независимого вычисления значения однонаправленной функции получателем сообщения в протоколе 1, метка времени tA должна передаваться дополнительно в открытом виде, а в сообщении 2 протокола 3 случайное число rA должно передаваться дополнительно в открытом виде.
Модифицированный вариант протокола 3 с учетом сформулированных изменений имеет структуру, изображенную на рис. 5.5.
Заметим, что в третье сообщение протокола включено поле А. Результирующий протокол обеспечивает взаимную аутентификацию и известен как протокол SKID 3.
5.3.2. СТРОГАЯ АУТЕНТИФИКАЦИЯ, ОСНОВАННАЯ
НА АСИММЕТРИЧНЫХ АЛГОРИТМАХ
В протоколах строгой аутентификации могут быть использованы асимметричные алгоритмы с открытыми ключами. В этом случае доказывающий может продемонстрировать знание секретного ключа одним из следующих способов:
— расшифровать запрос, зашифрованный на открытом ключе;
— поставить свою цифровую подпись на запросе.
Пара ключей, необходимая для аутентификации, не должна использоваться для других целей (например, для шифрования) по соображениям безопасности. Следует также предостеречь потенциальных пользователей о том, что выбранная система с открытым ключом должна быть устойчивой к атакам с выборкой шифрованного текста даже в том случае, если нарушитель пытается получить критичную информацию, выдавая себя за проверяющего и действуя от его имени.
Аутентификация с использованием асимметричных алгоритмов шифрования
В качестве примера протокола, построенного на использовании асимметричного алгоритма шифрования, можно привести следующий протокол аутентификации:
В качестве следующего примера приведем модифицированный протокол Нид-хэма и Шредера, основанный на асимметричном шифровании. Рассматривая вариант протокола Нидхэма и Шредера, используемый только для аутентификации, будем подразумевать под PB алгоритм шифрования открытым ключом участника В. Протокол имеет следующую структуру:
Аутентификация, основанная на использовании цифровой подписи
В рекомендациях стандарта Х.509 специфицирована схема аутентификации, основанная на использовании цифровой подписи, меток времени и случайных чисел.
Для описания данной схемы аутентификации введем следующие обозначения:
SA – подпись, сгенерированная участником A;
SB – подпись, сгенерированная участником В;
certA – сертификат открытого ключа участника A;
Если участники имеют аутентичные открытые ключи, полученные друг от друга, тогда можно не пользоваться сертификатами, в противном случае они служат для подтверждения подлинности открытых ключей.
В качестве примеров приведем следующие протоколы аутентификации:
1) Односторонняя аутентификация с применением меток времени:
После принятия данного сообщения участник В проверяет правильность метки времени tA, полученный идентификатор В и, используя открытый ключ из сертификата certA, корректность цифровой подписи SA(tA, В).
2) Односторонняя аутентификация с использованием случайных чисел:
Участник В, получив сообщение от участника A, убеждается, что именно он является адресатом сообщения; используя открытый ключ участника А, взятый из сертификата certA, проверяет корректность подписи SA(rA, rB, В) под числом rА, полученным в открытом виде, числом rB, которое было отослано в первом сообщении, и его идентификатором В. Подписанное случайное число rА используется для предотвращения атак с выборкой открытого текста.
3) Двусторонняя аутентификация с использованием случайных чисел:
В данном протоколе обработка сообщений 1 и 2 выполняется так же, как и в предыдущем протоколе, а сообщение 3 обрабатывается аналогично сообщению 2.
5.4. БИОМЕТРИЧЕСКАЯ АУТЕНТИФИКАЦИЯ ПОЛЬЗОВАТЕЛЯ
Процедуры идентификации и аутентификации пользователя могут базироваться не только на секретной информации, которой обладает пользователь (пароль, персональный идентификатор, секретный ключ и т. п.). Привычные системы аутентификации не всегда удовлетворяют современным требованиям в области информационной безопасности, особенно если речь идет об ответственных приложениях (онлайновые финансовые приложения, доступ к удаленным базам данных и т. п.).
В последнее время все большее распространение получает биометрическая аутентификация пользователя, позволяющая уверенно аутентифицировать потенциального пользователя путем измерения физиологических параметров и характеристик человека, особенностей его поведения. Использование решений, основанных на биометрической технологии, позволяет в ряде случаев улучшить положение дел в области аутентификации.
Для методов аутентификации, основанных на использовании многоразовых паролей, характерен следующий недостаток: многоразовый пароль может быть скомпрометирован множеством способов. Недостатком методов, связанных с использованием токенов (токен – компактное устройство в виде USB-брелока, которое служит для авторизации пользователя), является возможность потери, кражи, дублирования токенов – носителей критической информации. Биометрические методы, использующие для идентификации уникальные характеристики пользователя, свободны от перечисленных недостатков.
Отметим основные достоинства биометрических методов аутентификации пользователя по сравнению с традиционными:
— высокая степень достоверности аутентификации по биометрическим признакам из-за их уникальности;
— неотделимость биометрических признаков от дееспособной личности;
— трудность фальсификации биометрических признаков.
В качестве биометрических признаков, которые активно используются при аутентификации потенциального пользователя, можно выделить следующие:
— геометрическая форма кисти руки;
— форма и размеры лица;
— узор радужной оболочки и сетчатки глаз.
Рассмотрим типичную схему функционирования биометрической подсистемы аутентификации. При регистрации в системе пользователь должен продемонстрировать один или несколько раз свои характерные биометрические признаки. Эти признаки (известные как подлинные) регистрируются системой как «контрольный образ» (биометрическая подпись) законного пользователя. Этот образ пользователя хранится системой в электронной форме и используется для проверки идентичности каждого, кто выдает себя за соответствующего законного пользователя. В зависимости от совпадения или несовпадения совокупности предъявленных признаков с зарегистрированными в контрольном образе их предъявивший признается законным пользователем (при совпадении) или нет (при несовпадении).
С точки зрения потребителя, эффективность биометрической аутентификационной системы характеризуется двумя параметрами:
— коэффициентом ошибочных отказов FRR (false-reject rate);
— коэффициентом ошибочных подтверждений FAR (false-alarm rate).
Ошибочный отказ возникает тогда, когда система не подтверждает личность законного пользователя (типичные значения FRR составляют порядка одной ошибки на 100). Ошибочное подтверждение происходит в случае подтверждения личности незаконного пользователя (типичные значения FAR составляют порядка одной ошибки на 10000). Коэффициент ошибочных отказов и коэффициент ошибочных подтверждений связаны друг с другом; каждому коэффициенту ошибочных отказов соответствует определенный коэффициент ошибочных подтверждений.
В совершенной биометрической системе оба параметра ошибки должны быть равны нулю. К сожалению, биометрические системы не идеальны, поэтому приходится чем-то пожертвовать. Обычно системные параметры настраивают так, чтобы добиться требуемого коэффициента ошибочных подтверждений, что определяет соответствующий коэффициент ошибочных отказов.
К настоящему времени разработаны и продолжают совершенствоваться технологии аутентификации по отпечаткам пальцев, радужной оболочке глаза, по форме кисти руки и ладони, по форме и размеру лица, по голосу и «клавиатурному почерку».