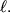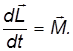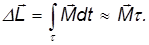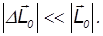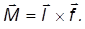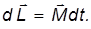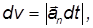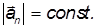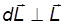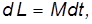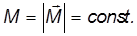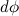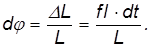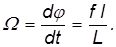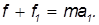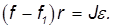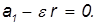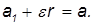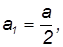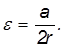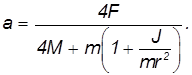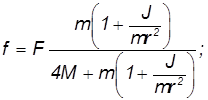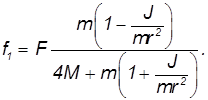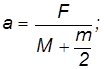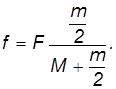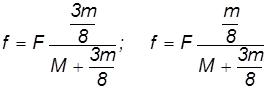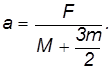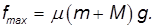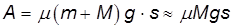При каком условии гироскоп начинает прецессировать чем определяется угловая скорость прецессии

Изучение гироскопа и определение угловой скорости прецессии гироскопа

Изучение гироскопа и определение угловой скорости прецессии гироскопа

Лабораторная работа № М11-н

И ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ ПРЕЦЕССИИ ГИРОСКОПА

Изучение динамики вращательного движения, закона сохранения момента импульса на примере вращения гироскопа. Ознакомление с гироскопическим эффектом и определение угловой скорости прецессии гироскопа.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Гироскопические приборы и системы применяются в различных областях техники: в авиации и на морских судах; в горнорудной и нефтяной промышленности (при прокладке шахт, тоннелей, при бурении скважин); в артиллерии и на танках для стабилизации прицелов и орудий и т. д.

В частности, успехи в области авиационной и ракетной техники стали возможными благодаря автоматизации процессов управления летательными аппаратами.

С помощью гироскопических приборов и систем решаются как задачи по управлению, ориентации, автономной навигации летательных объектов, так и проблемы по стабилизации и управлению специальных бортовых систем (антенны бортовых радиолокационных станций, чувствительные элементы головок самонаведения реактивных снарядов, авиационные прицелы и др.)

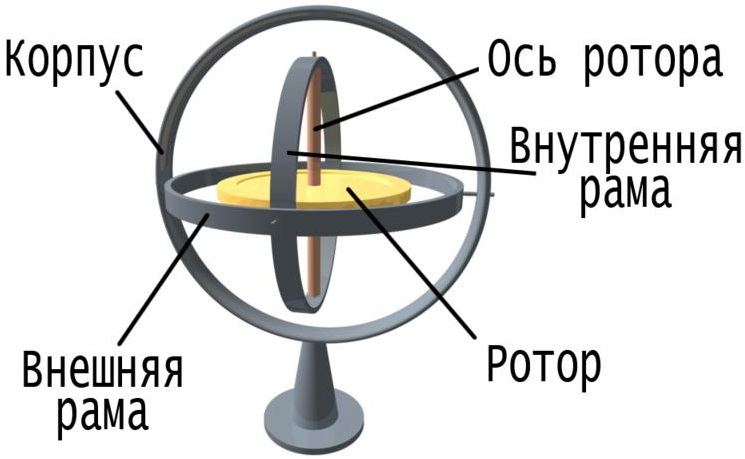
Гироскопические приборы и системы по назначению делятся на несколько групп. Применительно к теме данной лабораторной работы в гироскопических стабилизаторах используется свойство гироскопа сохранять неизменным направление своей оси вращения в пространстве.

Наибольшее применение имеют симметричные гироскопы, которые обладают осью симметрии, являющейся свободной осью вращения.

Отличительной особенностью свободных осей является то, что при вращении твердого тела вокруг любой из них момент импульса () совпадает по направлению с угловой скоростью ().

Следует отметить, что в общем случае направление векторов и не совпадают.

Вся теория гироскопа построена на уравнении моментов (втором законе динамики для вращательного движения), согласно которому производная момента импульса твёрдого тела по времени равна результирующему моменту внешних сил, действующих на тело

, (1)

причём моменты и определены относительно одной и той же точки заданной системы отсчёта (относительно неподвижной точки опоры гироскопа).

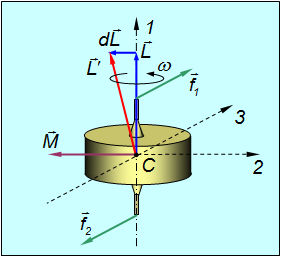
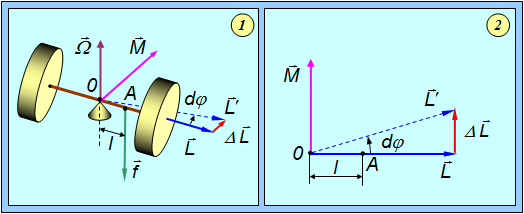
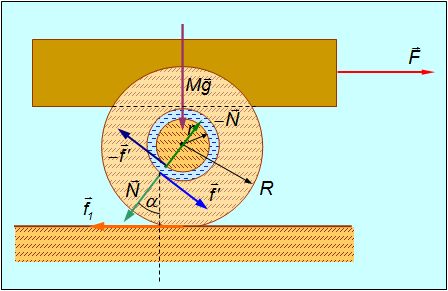
На волчок действует момент силы тяжести, стремящейся опрокинуть волчок, равный

, (2)

— угол, образованный осью волчка (гироскопа) с вертикалью (осью Z).

Вектор момента перпендикулярен к плоскости ОО1А, в которой находится сила тяжести .

Согласно (1) за время dt момент импульса волчка получит приращение, равное

(3)

в результате чего плоскость ОО1А, в которой расположены ось волчка и вектор , повернётся на угол

. (4)

Следует подчеркнуть, что вектор приращения момента импульса сонаправлен с вектором , т. е. .

Следовательно, вектор момента импульса , значит и ось волчка-гироскопа, будет поворачиваться вокруг вертикальной оси Z, описывая круговой конус с углом полураствора , причём вектор будет изменяться только по направлению, не меняясь по величине.

Итак, волчок-гироскоп будет прецессировать вокруг вертикальной оси Z с угловой скоростью прецессии, определяемой следующим образом.

Из рис.1 следует, что

. (5)

Учитывая, что величина момента импульса волчка-гироскопа равна * и, подставляя (2) в (5), получим согласно (4) выражение для вычисления угловой скорости прецессии:

,

(6)

Из (6) видно, что угловая скорость прецессии () не зависит от угла наклона оси волчка и, кроме того, подтверждается вышеуказанная закономерность: чем меньше угловая скорость () волчка, тем больше угловая скорость прецессии () или наоборот.

Следует отметить, что прецессионное движение имеет следующие особенности.

Во-первых, угловая скорость прецессии значительно меньше угловой скорости вращения гироскопа вокруг собственной оси, т. е. .

Во-вторых, из выражения =[] следует, что момент () определяет угловую скорость прецессии (), а не угловое ускорение. Следовательно, устранение момента приводит к мгновенному исчезновению прецессии, т. е. прецессия не обладает инертностью.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Принципиальная схема экспериментальной установки представлена на рис.2 и включает в свой состав: основание 1; корпус 2 с узлом подшипников, в котором установлен вал с коллектором; вилку 3, закреплённую на валу и предназначенную для крепления гироскопической системы; лимб 4; фотодатчики 5 и 6.

Гироскопическая система состоит из электродвигателя 9 с диском (маховиком) 10, стержня 11 и противовеса 12.

Лимб 4 предназначен для определения угла поворота гироскопической системы во время прецессии.

Стержень 11 и противовес 12 предназначены для создания свободной уравновешенной системы относительной оси и создания момента внешних сил, вызывающих прецессию гироскопа.

Фотодатчик 6 позволяет регистрировать частоту вращения оси гироскопа (ротора электродвигателя 9 с маховиком 10); фотодатчик 5 предназначен для выдачи сигналов при измерении времени поворота прецессирующей гироскопической системы.

Установка работает совместно с электронным блоком, на задней панели которого находится кнопка включения питания “СЕТЬ”.

УКАЗАНИЯ МЕР БЕЗОПАСНОСТИ

ПОДГОТОВКА УСТАНОВКИ КВЫПОЛНЕНИЮ ЭКСПЕРИМЕНТА

1.При помощи регулировочных опор 7 основания необходимо выставить его в горизонтальное положение.

3. При нажатии кнопки”СЕТЬ” электронного блокаэлектродвигатель с маховиком начинает раскручиваться и одновременно включаются табло индикации частоты вращения маховика гироскопа и таймер времени прецессии.

4. Кнопку ”+” на лицевой панели электронного блока следует удерживать в нажатом положении до момента, когда на левом табло блока установится показание частоты вращения маховика гироскопа, например, в диапазоне 29-31 Гц.(При необходимости можно воспользоваться кнопкой “-“).

5.Отпустите кнопку “+”, при этом табло будет показывать реальную (меньшую) частоту вращения маховика гироскопа, которая будет приближаться к установленной частоте по мере раскручивания маховика (время раскручивания маховика составляет 1-2 минуты ).

6. Убедитесь в отсутствии прецессии. Выключите питание лабораторной установки и дождитесть остановки маховика гироскопа.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ
ПРЕЦЕССИИ

Сместите противовес12 так, чтобы расстояние от конца стержня до ближайшей плоскости противовеса составило l1 = 30±0,5 мм, где l1–плечо неуравновешенного гироскопа.

Момент сил, вызывающих прецессию, равен

где m – масса противовеса с контргайкой;

=( l0–l1 ) =20мм.

После каждого измерения необходимо выключить установку, дождаться остановки маховика и установить гироскопическую систему в исходное состояние (см. пункт 2 ).

6.Выполните п. п. 2-5 не менее 5 раз при тех же значениях частоты вращения 30 Гц и 20 мм и результаты измерений занесите в табл. 1.

Угловая скорость прецессии может быть определена по формуле

?=?/?/2t, с-1 ( 8 )

* При проведении последующих измерений угол поворота гироскопической системы должен быть одинаковым, например, 10 град!

1,мм

Источник

При каком условии гироскоп начинает прецессировать чем определяется угловая скорость прецессии

Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.

Волчки. Устойчивость вращения симметричного волчка.

Свободный гироскоп.

В этом случае моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю. Это можно реализовать, например, поместив гироскоп в карданов подвес, описанный в лекции 3 и изображенный на рис. 3.13.

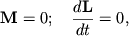(4.1)

и момент импульса сохраняется:

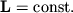(4.2)

Гироскоп ведет себя так же, как и свободнее тело вращения (см. лекцию 3). В зависимости от начальных условий возможны два варианта поведения гироскопа:

1. Если гироскоп раскручен вокруг оси симметрии, то направления момента импульса и угловой скорости совпадают:

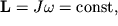(4.3)

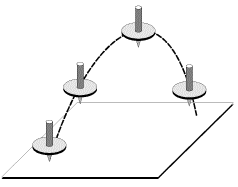Рис. 4.1.

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

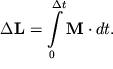(4.)

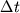
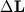
Если интервал времени мал, то и мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется «затвердевшим».

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 4.2). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места.. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.

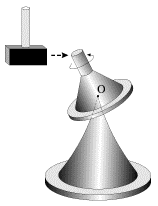Рис. 4.2.

2. Если свободный гироскоп раскручен так, что вектор мгновенной угловой скорости и ось симметрии гироскопа не совпадают (как правило, это несовпадение при быстром вращении бывает незначительным), то наблюдается движение, описанное в лекции 3 как «свободная регулярная прецессия». Применительно же к гироскопу его называют нутацией. При этом ось симметрии гироскопа, векторы L и лежат в одной плоскости, которая вращается вокруг направления с угловой скоростью, равной где — момент инерции гироскопа относительно главной центральной оси, перпендикулярной оси симметрии. Эта угловая скорость (назовем ее скоростью нутации) при быстром собственном вращении гироскопа оказывается достаточно большой, и нутация воспринимается глазом как мелкое дрожание оси симметрии гироскопа.

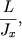
Прецессия гироскопа под действием внешних сил. Элементарная теория.

Рассмотрим теперь ситуацию, когда к оси гироскопа приложена сила, линия действия которой не проходит через точку закрепления. Опыты показывают, что в этом случае гироскоп ведет себя весьма необычным образом.

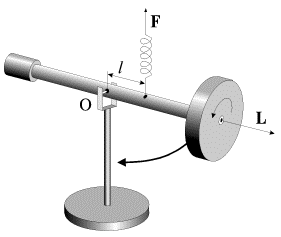Рис. 4.3.

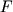
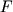
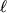
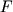
Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы (рис. 4.3), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением и ее плеча относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных и

Рис. 4.4.

Рис. 4.5.

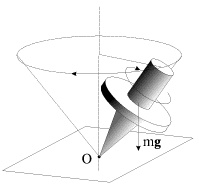
Точное решение задачи о движении гироскопа в поле внешних сил довольно выражение для угловой скорости прецессии можно легко получить в рамках так называемой элементарной теории гироскопа. В этой теории делается допущение, что мгновенная угловая скорость вращения гироскопа и его момент импульса направлены вдоль оси симметрии гироскопа. Другими словами, предполагается, что угловая скорость вращения гироскопа вокруг своей оси значительно больше угловой скорости прецессии:

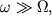(4.5)

так что вкладом в L, обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен

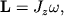(4.6)

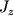
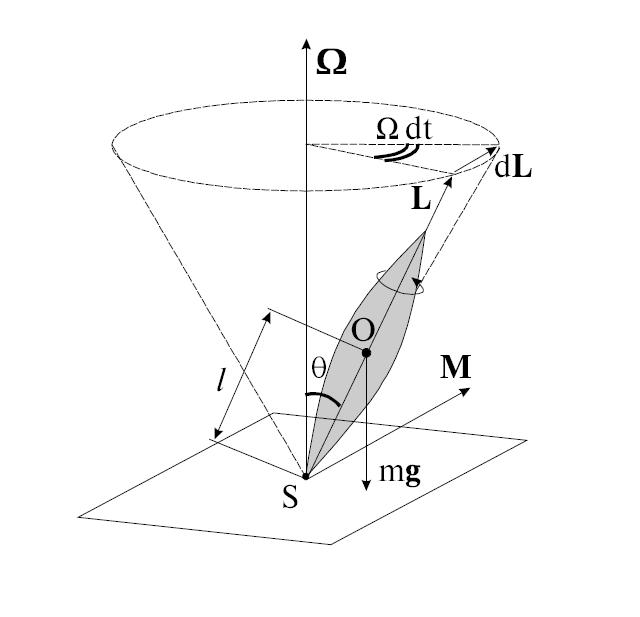
где — момент инерции относительно оси симметрии.

Итак, рассмотрим тяжелый симметричный гироскоп, у которого неподвижная точка S (точка опоры о подставку) не совпадает с центром масс О (рис. 4.6).

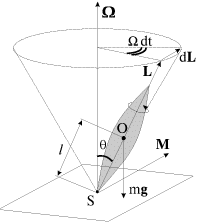Рис. 4.6.

Момент силы тяжести относительно точки S

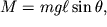(4.7)

Изменение момента импульса L определяется выражением

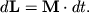(4.8)

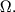
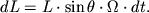При этом и L, и ось волчка прецессируют вокруг вертикального направления с угловой скоростью Еще раз подчеркнем: делается допущение, что выполнено условие (4.5) и что L постоянно направлен вдоль оси симметрии гироскопа. Из рис. 4.6 следует, что

(4.9)

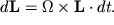(4.10)

Сравнивая (4.8) и (4.10), получаем следующую связь между моментом силы M, моментом импульса L и угловой скоростью прецессии :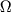

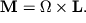(4.11)

Это соотношение позволяет определить направление прецессии при заданном направлении вращения волчка вокруг своей оси.

Обратим внимание, что M определяет угловую скорость прецессии, а не угловое ускорение, поэтому мгновенное «выключение» M приводит к мгновенному же исчезновению прецессии, то есть прецессионное движение является безынерционным.

Сила, вызывающая прецессионное движение, может иметь любую природу. Для поддержания этого движения важно, чтобы вектор момента силы M поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (4.11) (см. также рис. 4.6) можно получить:

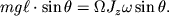(4.12)

Если учесть, что в нашем приближении справедливо соотношение (4.6), то для угловой скорости прецессии получим

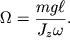(4.13)

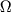
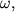
Следует отметить, что не зависит от угла наклона оси гироскопа и обратно пропорциональна что хорошо согласуется с опытными данными.

Источник

7.5. Гироскопы

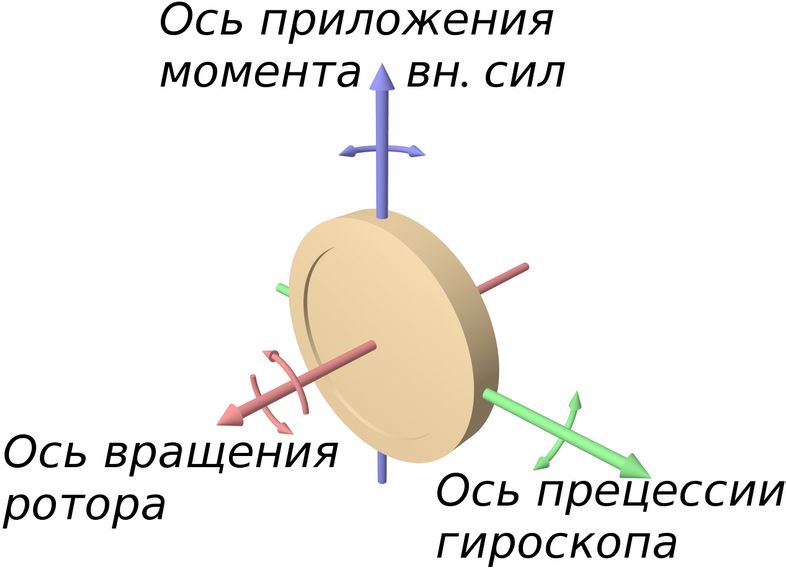
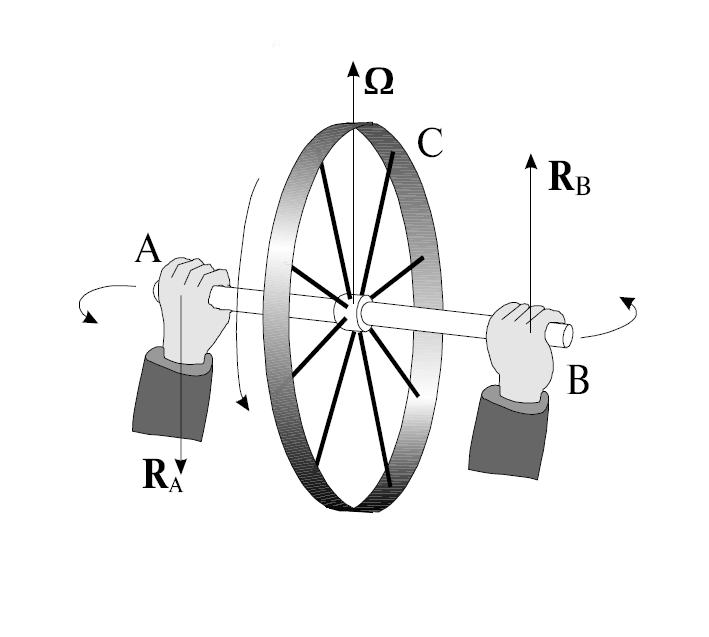
Гироскопом называется массивное осесимметричное тело (симметричный волчок), быстро вращающееся вокруг оси симметрии, причем ось вращения может изменять положение в пространстве. Ось симметрии называется осью фигуры гироскопа.

Видео 7.6. Что же такое гироскоп?

Рис. 7.17. Движение системы гироскопов

Ось симметрии является одной из главных осей гироскопа. Поэтому его момент импульса совпадает по направлению с осью вращения.

Для того, чтобы изменить положение в пространстве положение оси фигуры гироскопа, необходимо подействовать на него моментом внешних сил.

Видео 7.7. Гироскопические силы:большой гироскоп рвет веревку

Рис. 7.18. Направление векторов при вращении гироскопа

При этом наблюдается явление, получившее название гироскопического: под действием сил, которые, казалось бы, должны были вызвать поворот оси 1 вокруг оси 2 (рис. 7.19), наблюдается поворот оси фигуры вокруг оси 3.

Рис. 7.19. Движение оси фигуры гироскопа под действием момента внешних сил

Видео 7.8. Гироскоп с перегрузами: направление и скорость прецессии, нутации

Гироскопические явления проявляются всюду, где имеются быстро вращающиеся тела, ось которых может поворачиваться в пространстве.

Рис. 7.20. Реакция гироскопа на внешнее воздействие

Странное на первый взгляд поведение гироскопа, рис. 7.19 и 7.20, полностью объясняется уравнением динамики вращательного движения твердого тела

Видео 7.9. «Любвеобильный» гироскоп: ось гироскопа бежит вдоль направляющей, не покидая её

Видео 7.10. Действие момента силы трения: «Колумбово» яйцо

Если гироскоп привести в быстрое вращение, он будет обладать значительным моментом импульса. Если на гироскоп будет действовать внешняя сила в течение времени 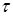, то приращение момента импульса будет

Если сила действует в течение короткого времени 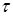, то

Другими словами, при коротких воздействиях (толчках) момент импульса гироскопа практически не меняется. С этим связана замечательная устойчивость гироскопа по отношению к внешним воздействиям, которая используется в различных приборах, таких как гирокомпасы, гиростабилизированные платформы и т. д.

Видео 7.11. Модель гирокомпаса, гиростабилизация

Видео 7.12. Большой гирокомпас

7.21. Гиростабилизатор орбитальной станции

В гироскопах, применяющихся в авиации и космонавтике, используется карданов подвес, который позволяет сохранять направление оси вращения гироскопа независимо от ориентации самого подвеса:

Видео 7.13. Гироскопы в цирке: езда на одном колесе по проволоке

http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 245–249 (§ 47): кинематическая теорема Эйлера о вращениях твердого тела вокруг неподвижной точки.

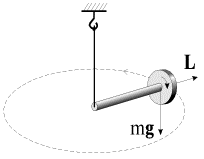
Рассмотрим движение гироскопа с неподвижной точкой опоры, как показано на на рис. 7.22.

Движение гироскопа под действием внешней силы называется вынужденной прецессией.

Рис. 7.22. Вынужденная прецессия гироскопа: 1 — общий вид; 2 — вид сверху

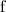
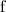
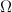
Приложим в точке А силу . Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы ось гироскопа будет вращаться с угловой скоростью вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.

Таким образом, прецессия гироскопа представляет собой движение под действием внешних сил, происходящее таким образом, что ось фигуры описывает коническую поверхность.

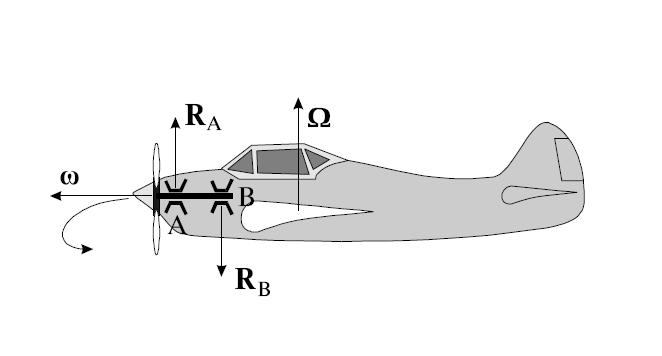
Рис. 7.23. К выводу формулы прецессии гироскопа.

Объяснение этого явления заключается в следующем. Момент силы 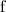относительно точки 0 будет

Приращение момента импульса гироскопа за время 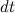равно

Это приращение перпендикулярно моменту импульса и, следовательно, меняет его направление, но не величину.

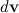
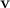
Вектор момента импульса ведет себя подобно вектору скорости при движении частицы по окружности. В последнем случае приращения скорости перпендикулярно скорости частицы и равно по модулю

В случае гироскопа элементарное приращение момента импульса

За время 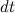вектор момента импульса повернется на угол

Угловая скорость вращения плоскости, проходящей через ось конуса, описываемого осью фигуры, и ось фигуры, называется угловой скоростью прецессии гироскопа.

Возникающие при определенных условиях колебания оси фигуры гироскопа в плоскости, проходящей через ось указанного выше конуса и саму ось фигуры, называются нутациями. Нутации могут быть вызваны, например, коротким толчком оси фигуры гироскопа вверх или вниз (см. рис. 7.24):

Рис. 7.24. Нутации гироскопа

Угловая скорость прецессии в рассматриваемом случае равна

Отметим важное свойство гироскопа — его безынерционность, заключающееся в том, что после прекращения действия внешней силы вращение оси фигуры прекращается.

http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 288–293 (§ 52): изложены основы точной теории гироскопа.

http://femto.com.ua/articles/part_1/0796.html — физическая энциклопедия. Описаны разнообразные механические гироскопы, которые используются для навигации — гирокомпасы.

http://femto.com.ua/articles/part_1/1901.html — физическая энциклопедия. Описан лазерный гироскоп для целей космической навигации.

Влияние гироскопических сил в технике иллюстрируется следующими рисунками.

Рис. 7.25. Гироскопические силы,действующие на самолет при вращении винта

Рис. 7.26. Перевертывание волчка под действием гироскопических сил

Рис. 7.27. Как поставить яйцо «на попа»

http://www.pereplet.ru/nauka/Soros/pdf/9809_096.pdf — Соросовский образовательный журнал, 1998 г., № 9, — в статье обсуждаются проблемы динамики вращающихся тел (кельтских камней), соприкасающихся с твердой поверхностью (А.П. Маркеев).

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_35.djvu — Михайлов А.А. Земля и ее вращение, Библиотечка Квант, выпуск 35 стр. 50–56 — планета Земля — большой волчок, ее ось прецессирует в пространстве.

О принципе работы колеса

Раз уж мы много говорили в этой главе о вращении тел, остановимся на самом великом и важном открытии человечества — изобретении колеса. Всем известно, что волочить груз гораздо труднее, чем перевозить его на колесах. Встает вопрос, почему? Колесо, играющее огромную роль в современной технике, по праву считается одним из гениальнейших изобретений человечества.

Передвижение груза с помощью катка. Прототипом колеса был каток, подкладываемый под груз. Его первые применения теряются во мгле веков. Прежде чем разбираться с колесом, поймем принцип действия катка. Для этого рассмотрим пример.

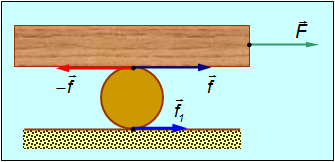
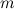
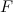
Пример. Груз массой M положен на цилиндрический каток массой и радиусом , который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила (рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.

Рис. 7.28. Передвижение груза с помощью катка

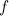
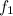
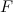
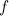
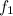
Обозначим силу трения между катком и грузом и — между катком и настилом. За положительное направление примем направление внешней силы . Тогда положительным значениям и соответствуют направления сил трения, показанные на рис. 7.28.

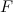
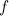
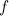
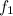
Таким образом, на груз действуют силы и , а на каток — силы и . Обозначим a ускорение груза и a₁ — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением .

Уравнения поступательного движения принимают вид:

Уравнение вращательного движения катка записывается так:

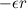
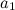
Обратимся теперь к условиям отсутствия проскальзывания. Из-за вращения катка его нижняя точка имеет линейное ускорение и, кроме того, участвует в поступательном движении с ускорением . В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что

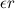
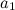
Верхняя точка катка приобретает из-за вращения противоположно направленное линейное ускорение и то же ускорение поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:

Из полученных уравнений для ускорений следует, что ускорение катка в два раза меньше ускорения груза:

Из непосредственного опыта каждый знает, что каток действительно отстает от груза.

Подставляя соотношения для ускорений в уравнения движения и решая их относительно неизвестных , , , получаем следующие выражение для ускорения груза

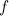
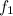
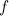
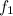
Обе силы трения и оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:

Как видно, радиус катка особой роли не играет: отношение зависит только от его формы. При данных массе и радиусе момент инерции катка максимален, когда каток представляет собой трубу: . В этом случае сила трения между катком и настилом отсутствует ( = 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:

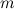
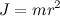
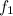
При уменьшении массы катка сила трения уменьшается, ускорение груза увеличивается — груз легче перемещать.

В случае катка-цилиндра (бревна) 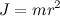/2 и мы находим силы трения

Сравнивая с результатами для катка-трубы, видим, что эффективно масса катка как бы уменьшилась: ускорение груза возрастает при прочих равных условиях.

Главный итог рассмотренного примера: ускорение отлично от нуля (то есть груз начинает двигаться) при сколь угодно малой внешней силе. При волочении же груза по настилу для его смещения необходимо приложить как минимум силу .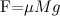

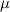
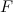
Второй вывод: ускорение вовсе не зависит от величины трения между частями данной системы. Коэффициент трения не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила не должна быть слишком велика.

Полученный результат, что каток как бы полностью «уничтожает» силу трения, не удивителен. Действительно, в отсутствие относительного перемещения соприкасающихся поверхностей силы трения не совершают работы. На самом деле каток «заменяет» трение скольжения на трение качения, которым мы пренебрегли. В реальном случае минимальная сила, необходимая для движения системы, отлична от нуля, хотя и гораздо меньше, чем при волочении груза по настилу. В современной технике принцип действия катка реализуется в шарикоподшипниках.

Качественное рассмотрение работы колеса. Разобравшись с катком, перейдем к колесу. Первое колесо в виде деревянного диска, насаженного на ось, появилось, по-видимому, в IV тысячелетии до н.э. в цивилизациях Древнего Востока. Во II тыс. до н.э. конструкция колеса совершенствуется: появляются спицы, ступица и гнутый обод. Изобретение колеса дало гигантский толчок развитию ремесел и транспорта. Однако многие не понимают самого принципа действия колеса. В ряде учебников и энциклопедий можно найти неверное утверждение, что колесо, подобно катку, также дает выигрыш, заменяя силу трения скольжения на силу трения качения. Иногда приходится слышать ссылки на использование смазки или подшипников, но дело не в этом, поскольку колесо с очевидностью появилось раньше, чем додумались до смазки (и, тем более, подшипников).

Действие колеса проще всего понять, исходя из энергетических соображений. Древние повозки устроены просто: кузов прикрепляется к деревянной оси радиусом (общая масса кузова с осью равна M). На ось насаживаются колеса массой и радиусом R (рис. 7.29).

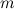
Рис. 7.29. Передвижение движение груза с помощью колеса

Работа против этой силы равна

(так как обычно масса колес много меньше массы повозки

Источник