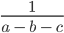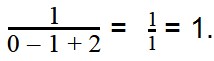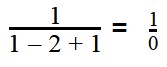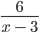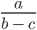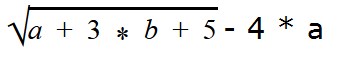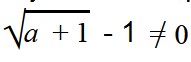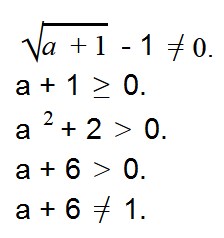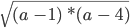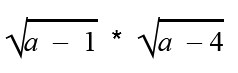При этом говорят что число 3 переменной x
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение 
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ: 
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение 
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение 
Пример 3
Рассмотрим выражение 
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения 
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 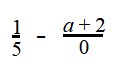— пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении 
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении 
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля — 
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение 
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду 
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
При этом говорят что число 3 переменной x
var a = 2;
if (a == 0 || a ==2) <
a += 7;
> else <
a /= 10;
>
alert(a);
13. Если переменная a равна или меньше 1, а переменная b больше или равна 3, то выведите сумму этих переменных, иначе выведите их разность (результат вычитания). Проверьте работу скрипта при a и b, равном 1 и 3, 0 и 6, 3 и 5.
var a = 3;
var b = 5;
if (a =3) <
alert(+a+b);
> else <
alert(a-b);
>
14. Если переменная a больше 2-х и меньше 11-ти, или переменная b больше или равна 6-ти и меньше 14-ти, то выведите ‘Верно’, в противном случае выведите ‘Неверно’.
15. Переменная num может принимать 4 значения: 1, 2, 3 или 4. Если она имеет значение ‘1’, то в переменную result запишем ‘зима’, если имеет значение ‘2’ – ‘весна’ и так далее. Решите задачу через switch-case.
var num = 4;
var result;
switch (num) <
case 1:
result = «Зима»;
break;
case 2:
result = «Весна»;
break;
case 3:
result = «Лето»;
break;
case 4:
result = «Осень»;
break;
default:
alert(«Введите число от 1 до 4»);
break;
>
16. В переменной day лежит какое-то число из интервала от 1 до 31. Определите в какую декаду месяца попадает это число (в первую, вторую или третью).
17. В переменной month лежит какое-то число из интервала от 1 до 12. Определите в какую пору года попадает этот месяц (зима, лето, весна, осень).
var str = «abcde»;
if (str[0] == «a») <
alert(«Да»);
> else <
alert(«Нет»);
>
var str = «12345»;
if (str[0] == «1» || str[0] == «2» || str[0] == «3») <
alert(«Да»);
> else <
alert(«Нет»);
>
20. Дана строка из 3-х цифр. Найдите сумму этих цифр. То есть сложите как числа первый символ строки, второй и третий.
var str = «763»;
alert(Number(str[0]) + Number(str[1]) + Number(str[2]));
var str = «864372»;
if ((Number(str[0]) + Number(str[1]) + Number(str[2])) == (Number(str[3]) + Number(str[4]) + Number(str[5]))) <
alert(«Да»);
> else <
alert(«Нет»);
>
var str = «864372»;
var sum1 = Number(str[0]) + Number(str[1]) + Number(str[2]);
var sum2 = Number(str[3]) + Number(str[4]) + Number(str[5])
if (sum1 == sum2) <
alert(«Да»);
> else <
alert(«Нет»);
>
Строк больше, но читаемость лучше.
Урок №4. Работа с циклами for и while в JavaScript.
1. Выведите столбец чисел от 1 до 100.
for (var i = 1; i Нравится Показать список оценивших
При этом говорят что число 3 переменной x
Логическая функция F задаётся выражением (¬x ≡ z) → (y ≡ (w ∨ x)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|
| Переменная 1 | Переменная 1 | Функция |
|---|
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. | Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке | Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
| ID магазина | Район | Адрес |
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите, сколько литров молока безлактозного было продано в магазинах Октябрьского района за период с 1 по 10 июня включительно.
В ответе запишите только число. Ответ округлите до десятых.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу. Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:
Вперед 5 – Кузнечик прыгает вперёд на 5 единиц,
Назад 3 – Кузнечик прыгает назад на 3 единицы.
Какое наименьшее количество раз должна встретиться в программе команда «Назад 3», чтобы Кузнечик оказался в точке 21?
Определите, что будет напечатано в результате работы следующего фрагмента программы:
DIM N, S AS INTEGER
using namespace std;
Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 150 Мбайт данных, причем первую половину времени передача шла со скоростью 2 Мбит в секунду, а остальное время — со скоростью 6 Мбит в секунду?
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
Запишите слово, которое стоит на 210-м месте от начала списка.
Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Сколько раз встречалась температура, которая была ниже половины от максимального значения?
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «свет» или «Свет» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «свет», такие как «светло», «светает» и т. д., учитывать не следует. В ответе укажите только число.
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 9 символов. Из соображений информационной безопасности каждый пароль должен содержать хотя бы 1 десятичную цифру, как прописные, так и строчные латинские буквы (в латинском алфавите 26 букв), а также не менее 1 символа из 6-символьного набора: «&», «#», «$», «*», «!», «@». В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей.
Для хранения сведений о 20 пользователях потребовалось 500 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число – количество байт.
Примечание. В латинском алфавите 26 букв.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
| вверх | вниз | влево | вправо |
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ (также по отношению к наблюдателю):
| сверху свободно | снизу свободно | слева свободно | справа свободно |
выполняется, пока условие истинно.
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
ПОКАснизу свободно ИЛИ справа свободно
ПОКА справа свободно
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
procedure F(n: integer);
Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(5). Числа должны быть записаны в том же порядке, в котором они выводятся на экран.
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает Определите и запишите в ответе сначала количество пар элементов последовательности, для которых произведение элементов делится без остатка на 62, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
Дан квадрат 15 × 15 клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата стоит ладья. За один ход ладья может переместиться в пределах квадрата на любое количество клеток вправо или вниз (влево и вверх ладья ходить не может). Необходимо переместить ладью в правый нижний угол так, чтобы сумма чисел в клетках, в которых ладья останавливалась (включая начальную и конечную), была минимальной. В ответе запишите минимально возможную сумму.
Исходные данные записаны в электронной таблице.
Пример входных данных (для таблицы размером 4 × 4):
| −6 | 3 | −3 | 1 |
| 1 | −3 | 3 | −5 |
| −4 | 4 | −2 | 2 |
| 5 | 0 | 0 | 3 |
Для указанных входных данных ответом будет число −10 (ладья проходит через клетки с числами −6, 1, −3, −5, 3).
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 10 камней. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 17 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 31 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 30.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 10 камней. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 17 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 31 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 30.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 10 камней. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 17 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 31 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 30.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
- При этом в сосуде появляется туман что означает что температура воздуха
- При этом следует отметить что