представление информации в двоичном коде информации
Информатика. 7 класс
Конспект урока
Кодирование информации. Двоичный код
Перечень вопросов, рассматриваемых в теме:
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Теоретический материал для самостоятельного изучения
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.
Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.
Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.
Обратите внимание, что:
32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:
В математике такие произведения записывают в виде:
Запись 2 i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Универсальность двоичного кодирования
В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.
Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Разбор решения заданий тренировочного модуля
№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Переведите десятичное число 273 в двоичную систему счисления.
Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Ответ: 27310= 100010001.
№2. Тип задания: единичный / множественный выбор.
Четыре буквы латинского алфавита закодированы кодами различной длины:
Курс лекций по теме «Двоичное кодирование информации»
Двоичное кодирование информации.
Естественные и формальные языки.
Знаки могут иметь различную физическую природу, например, для письма служат знаки, которые являются изображением на бумаге, а при обработке текста на компьютере знаки представляются в виде последовательностей электрических импульсов (т. е. некоторым образом кодируются). Вообще, кодированием называется представление символов одного алфавита символами другого. В качестве простейшей системы кодирования можно привести известную всем азбуку Морзе.
В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации.
1. Двоичное кодирование информации.
В настоящее время созданы технические устройства, которые могут надежно сохранять и распознавать информацию, закодированную с помощью всего двух состояний (т.е. в двоичной системе кодирования):
— Поверхности магнитных носителей информации (намагничено/размагничено);
— Поверхности лазерных дисков (отражает/не отражает);
— Триггер, который может находиться в одном из двух состояний О или 1, широко используется в оперативной памяти компьютера.
Таким образом, в компьютерах используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
— представление информации посредством только двух состояний надежно и помехоустойчиво;
— возможно применение аппарата алгебры логики для выполнения логических преобразований информации;
2. Двоичное кодирование текстов. Кодовые таблицы.
При вводе в компьютер текстовой информации каждая буква кодируется определенным числом, а при выводе на внешние устройства (экран или печать) для восприятия человеком по этим числам строятся изображения букв. Соответствие между набором букв и числами называется кодировкой символов.
Традиционно для кодирования одного символа используется количество информации, равное 1 байту (8 битам). Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код (или соответствующий ему двоичный код). Код символа хранится в памяти компьютера, где занимает, как уже говорилось, 1 байт. При таком способе можно закодировать 256 различных символов (256 = 2 8 ). Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и заглавные буквы русского алфавита, цифры, знаки, графические символы и т. д.
Каждому символу такого алфавита ставится в соответствие уникальный десятичный код от 0 до 255, а каждому десятичному коду соответствует 8-разрядный двоичный код от 00000000 до 11111111. Таким образом, компьютер различает символы по их коду.
Для разных типов ЭВМ и операционных систем используются различные таблицы кодировки, отличающиеся порядком размещения символов алфавита в кодовой таблице.
В настоящее время существует несколько различных кодировок (кодовых таблиц) для русских букв. Поэтому если текст создан в одной кодировке, то он не будет правильно отображаться в другой.
Понятно, что каждая кодировка задается своей кодовой таблицей. Одному и тому же двоичному коду в различных кодировках соответствуют различные символы.
Для того чтобы стало возможным чтение и редактирования текста, набранного в другой кодировке, используются программы перекодирования русского текста. Некоторые текстовые редакторы (например, MS Word и др.) содержат встроенные программы-конверторы, позволяющие читать текст в различных кодировках.
Присвоение символу конкретного кода является вопросом соглашения, которое и фиксируется в конкретной кодовой таблице. В качестве международного стандарта принята кодовая таблица ASCII. В этой кодовой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов.
Стандартными в этой таблице кодов ASCII являются только первые 128 символов, т. е. символы с номерами от нуля (двоичный код 00000000) до 127 (01111111). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, начиная со 128 (двоичный код 10000000) и кончая 255 (11111111), используются для кодировки букв национальных алфавитов, символов псевдографики и научных символов.
3. Двоичное кодирование звуковой информации.
Поступим следующим образом. Будем измерять напряжение через равные промежутки времени и записывать полученные значения в память компьютера. Этот процесс и есть дискретизация (или оцифровка). Для того чтобы воспроизвести закодированный таким образом звук, нужно выполнить обратное преобразование, а затем сгладить получившийся ступенчатый сигнал.
Итак, в процессе кодирования звуковой информации происходит временная дискретизация звука (когда звуковая волна разбивается на отдельные маленькие временные участки). Для каждого такого участка устанавливается определенная величина амплитуды. Таким образом, непрерывная зависимость амплитуды сигнала от времени заменяется дискретной последовательностью уровней громкости. Уровни громкости звука можно рассматривать как набор возможных состояний. Чем больше уровней громкости может быть выделено в процессе оцифрования, тем более качественным будет звучание.
Ясно, что качество кодирования будет напрямую зависеть от количества измерений уровня сигнала в единицу времени. Этот показатель называется частотой дискретизации . Чем выше частота дискретизации (т. е. количество отсчетов за секунду) и чем больше разрядов отводится для каждого отсчета, тем точнее будет представлен звук. Но при этом увеличивается и размер звукового файла.
Итак, по окончании процесса дискретизации, звуковая информация хранится в памяти компьютера в виде двоичных кодов. При этом качество двоичного кодирования звуковой информации определяется двумя показателями: глубиной кодирования и частотой дискретизации.
Описанный способ кодирования звуковой информации достаточно универсален, он позволяет представить любой звук и преобразовывать его самыми разными способами. С помощью программ для компьютера можно выполнить, например, такое преобразование полученной информации, как «наложение» друг на друга звуков от разных источников, изменение музыкального темпа и т. д.
4. Двоичное кодирование графической информации.
При оцифровке изображения оно делится на такие крошечные ячейки, что глаз человека их не видит, воспринимая все изображение как целое. Сама сетка получила название растровой карты (или растра), а ее единичный элемент называется пикселем. Пиксели подобны зернам фотографии и при значительном увеличении они становятся заметными.
Количество различных цветов — К и количество битов для их кодировки — N связаны между собой простой формулой: 2 N = К.
Таким образом, цвет каждого пикселя кодируется определенным числом битов, то есть элементарных единиц информации, с которыми может иметь дело компьютер. Количество битов, используемых для кодирования цвета точки, называется глубиной цвета.
Совокупность всех используемых цветов называется палитрой цветов. Для получения богатой палитры цветов базовым цветам могут быть заданы различные интенсивности. Так, например, при глубине цвета 24 бита на кодирование каждого из цветов выделяется по 8 бит, т. е. для каждого из цветов возможны n = 2 8 = 256 уровней интенсивности.
Двоичное кодирование информации
Любая информация внутри компьютера хранится и обрабатывается в виде длинного кода, состоящего всего из двух символов. Этот код называется двоичным или бинарным.
По своей сути он очень похож на всем известный код Морзе, в котором двумя символами (длинный и короткий импульс) шифруются буквы для передачи текстовой информации по проводам или другим способом.
Компьютеры же пошли значительно дальше. В них в форме бинарного кода хранятся не только текстовые данные, но и программы, музыка, изображения и даже видео высокой четкости.
Перед выводом информации на экран, в аудиосистему или распечатыванием, компьютер «переводит» ее в понятный человеку язык. Но внутри компьютера она хранится и обрабатывается исключительно в виде двоичного кода.
Если вы не программист, знать систему использования бинарного кода в совершенстве не обязательно. Для понимания принципов работы компьютера достаточно разобраться с вопросом в общих чертах. В этом вам и поможет предлагаемая статья.
Содержание статьи
Почему в компьютере используется двоичный код
Люди для записи текстовой информации используют буквы. В русском языке их 33. Комбинациями из десяти цифр (от 0 до 9) мы записываем числовые данные. При работе с графической информацией пользуемся палитрой из миллионов цветов. Наши уши различают звуки в диапазоне от 16 до 20000 Гц.
Если добавить к этому обоняние, вкусовые и тактильные ощущения, получится огромнейшее разнообразие информационных импульсов, которые может воспринимать, хранить и обрабатывать наш мозг.
При помощи технических средств невозможно воссоздать аналогичную систему работы с информацией.
Людям проще всего создавать приборы, принимающие одно из двух состояний: лампочка горит или нет, магнитное поле есть или его нет и т.д. И значительно сложнее, например, заставить лампочку в разных ситуациях светиться одним из 10 цветов. Не говоря уже о 10 миллионах цветов, воспринимаемых человеком.
В технике намного удобнее иметь дело с множеством простых элементов, чем с небольшим количеством сложных.
Чтобы иметь возможность хранить и обрабатывать информацию техническими средствами, люди решили переводить ее на максимально простой «язык», состоящий всего из двух «букв» – так называемый двоичный или бинарный код.
Используя разные комбинации большого количества двух символов, в бинарном коде можно зашифровать любую числовую, текстовую, звуковую или графическую информацию.
Компьютер же является ничем иным, как машиной, предназначенной для хранения и обработки информации в таком виде.
Перевод данных в двоичный код называется кодированием.
Противоположный процесс, в результате которого бинарный код превращается в привычную для людей информацию, называется декодированием.
Компьютер осуществляет кодирование «на лету» при получении данных извне: ввод текста пользователем с клавиатуры, запись видео с веб-камеры, запись звука с микрофона и т.д.
Перед выводом информации на экран, в аудиосистему или же ее распечатыванием, происходит обратный процесс (декодирование).
Как осуществляется кодирование различных типов данных, рассмотрим немного ниже. Сначала давайте разберемся, из каких же символов формируется двоичный код внутри компьютера и как он там хранится.
С технической стороны компьютерный двоичный код реализуется наличием или отсутствием определенных свойств (импульсов) у мельчайших запоминающих элементов. Эти импульсы могут быть:
• фотооптическими
Так, поверхность любого оптического диска (CD, DVD или BluRay) состоит из спирали, которую формируют мелкие отрезки. Каждый из них может быть либо темного, либо светлого цвета. Диск быстро вращается в дисководе. На его спиральной дорожке фокусируется лазер, отражение которого попадает на фотоэлемент. Темные участки спирали поглощают свет и не передают его на фотоэлемент, светлые – наоборот, отражая свет, передают импульс фотоэлементу. В результате фотоэлемент получает информацию, зашифрованную в дорожке диска в виде темных и светлых точек.
Например, внутри жесткого диска находится быстро вращающаяся пластина. Вся ее поверхность тоже представляет собой спираль, состоящую из последовательности миллионов мелких участков. Каждый из них является элементом, который может принимать одно из двух состояний: «намагниченное», «ненамагниченное». Эти элементы и формируют двоичный код, в котором кодируется какая-то информация. Считывание состояния элементов осуществляется специальной головкой, которая быстро движется по поверхности пластины;
Например, оперативная память компьютера является микросхемой, состоящей из миллионов маленьких ячеек, созданных из микроскопических транзисторов и конденсаторов. Каждая такая ячейка может либо содержать электрический заряд, либо нет. Комбинации заряженных и разряженных ячеек оперативной памяти и формируют в ней двоичный код.
В аналогичной форме информация хранится и во всех других запоминающих микросхемах (флешки, SSD-носители и др.).
Процессор компьютера обрабатывает двоичный код тоже в виде электрических импульсов.
Иногда можно встретить ошибочное мнение, что бинарный код внутри компьютера записан в виде обычных нулей и единиц. Это следствие непонимания технической стороны вопроса. Привычных для нас нулей и единиц в компьютере нет. «Символами» компьютерного двоичного кода является наличие или отсутствие у мельчайшего запоминающего элемента определенного свойства (см. выше).
Чтобы было нагляднее, в учебных материалах отсутствие у элемента такого свойства лишь условно обозначают нулем, а его наличие – единицей. Но с таким же успехом их можно бы было обозначать точкой и тире или крестиком и ноликом.
Единицы компьютерной информации
В предыдущем пункте уже говорилось о том, что бинарный код внутри компьютера хранится в виде комбинаций большого количества элементов, каждый из которых может иметь одно из двух состояний.
Такой мельчайший элемент, участвующий в формировании бинарного кода, называется битом.
Битом является, например, каждая темная или светлая точка дорожки оптического диска, каждая запоминающая ячейка оперативной памяти компьютера и т.д.
Но каждый отдельный бит сам по себе не имеет практической ценности. Для кодирования информации используются блоки из нескольких битов.
Представим, например, что в каком-то запоминающем устройстве содержится только один бит. В нем можно будет закодировать всего одно из двух состояний чего либо, например, одну из двух цифр или один из двух цветов. Понятное дело, что практическая ценность такого носителя минимальна.
Блок из 2 битов может принимать одно из 4 состояний:
В 3-хбитном блоке можно закодировать уже одно из 8 состояний:
Ну а 8-битный блок может принимать аж 256 разных состояний. Это уже достаточно существенная частичка двоичного кода, позволяющая отобразить один из значительного количества вариантов.
Например, каждому состоянию 8-битного блока можно сопоставить какую-то букву. Вариантов, а их 256, будет достаточно для кодирования всех русских букв, включая строчные и прописные их варианты, а также всех знаков препинания. Заменяя каждую букву соответствующим 8-мибитным блоком, из двоичного кода можно составить текст.
Этот принцип и используется для записи в компьютере текстовой информации (подробнее речь об этом пойдет ниже).
Как видите, 8-битная ячейка имеет вполне реальную практическую ценность. Поэтому ее и решили считать минимальной единицей компьютерной информации. Эта единица получила название байт.
Текстовые файлы состоят из сотен, тысяч или даже десятков тысяч букв. Соответственно, для их хранения в двоичном коде требуются сотни, тысячи или десятки тысяч байтов.
Поэтому на практике гораздо чаще приходится имеет дело не с байтами, а с более крупными единицами:
• килобайтами (1 килобайт = 1024 байт);
• мегабайтами (1 мегабайт = 1024 килобайт);
• гигабайтами (1 гигабайт = 1024 мегабайт);
• терабайтами (1 терабайт = 1024 гигабайт).
Кодирование числовой информации
Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: 0 1 2 3 4 5 6 7 8 9. Эта система называется десятичной.
Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до 9), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до 99, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до 999 и т.д.
Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.
Система счисления, использующая только две цифры, называется двоичной.
При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.
Вот таблица первых десяти чисел в каждой из этих систем счисления:
Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно 1 разряда. В двоичной системе для тех же целей потребуется уже 4 разряда.
Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум 4 бита (0,5 байта).
Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:
• небольшие целые числа без знака
Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется 1 байт (8 битов). Запись осуществляется в полной аналогии с двоичной системой счисления.
Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:
• большие целые числа и числа со знаком
Для записи каждого такого числа на запоминающем устройстве, как правило, отводится 2-байтний блок (16 битов).
Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком «плюс», этот бит остается пустым, если со знаком «минус» – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах.
Например, алгоритм кодирования числа +2676 будет следующим:
1. Перевести число 2676 из десятичной системы счисления в двоичную. В итоге получится 101001110100;
2. Записать полученное двоичное число в первые 15 бит 16-битного блока (начиная с правого края). Последний, 16-й бит, должен остаться пустым, поскольку кодируемое число имеет знак +.
В итоге +2676 в двоичном коде на запоминающем устройстве будет выглядеть так:
Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.
1. Перевести число 2676 из десятичной системы счисления в двоичную. Получим все тоже двоичное число 101001110100;
2. Записать полученное двоичное число в первые 15 бит 16-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из 15 битов;
3. Записать в 16-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.
Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.
Максимальным десятичным числом, которое можно закодировать в 15 битах запоминающего устройства, является 32767. Иногда для записи чисел по этому алгоритму выделяются 4-байтные блоки. В таком случае для кодирования каждого числа будет использоваться 31 бит плюс 1 бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет 2147483647 (со знаком плюс или минус).
• дробные числа со знаком
Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.
Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет 4-байтную ячейку (32 бита):
• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком «плюс» – бит остается пустым.
• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
• в следующих за ним 7 битах записывается значение порядка.
• в оставшихся 23 битах записывается так называемая мантисса числа.
Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число 6,25.
Порядок кодирования будет примерно следующим:
1. Перевести десятичное число в двоичное (десятичное 6,25 равно двоичному 110,01);
3. Определить значение и знак порядка.
Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно 3 (или 11 в двоичной форме);
Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс»;
Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается.
Числа с плавающей запятой, кодируемые в 32 битах, называю числами одинарной точности.
Когда для записи числа 32-битной ячейки недостаточно, компьютер может использовать ячейку из 64 битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.
Двоичное кодирование текстовой информации
Существует несколько общепринятых стандартов кодирования текста в двоичном коде.
Одним из наиболее «старых» (разработан еще в 1960-х гг.) является стандарт ASCII (от англ. American Standard Code for Information Interchange). Это 7-битный стандарт кодирования. То есть, используя его, компьютер записывает каждую букву или знак в одну 7-битную ячейку запоминающего устройства.
Как известно, ячейка из 7 битов может принимать 128 различных состояний. Соответственно, в стандарте ASCII каждому из этих 128 состояний соответствует какая-то буква, знак препинания или специальный символ.
Дальнейшее развитие компьютерной техники показало, что 7-битный стандарт кодирования является слишком «тесным». В 128 состояниях, принимаемых 7-битной ячейкой, невозможно закодировать буквы всех существующих в мире письменностей.
Восьмибитными кодировками, распространенными в нашей стране, являются KOI8, UTF8, Windows-1251 и некоторые другие.
Разработаны также и универсальные стандарты кодирования текста (Unicode), включающие буквы большинства существующих языков. В них для записи одного символа может использоваться до 16 битов и даже больше.
Существование большого количества кодировок текста является причиной многих проблем. Вы, наверное, уже встречались с ситуацией, когда в некоторых программах на экране вместо букв отображаются непонятные «кракозябры». Это потому, что компьютер иногда «ошибается» и неверно определяет кодировку, в которой этот текст хранится в его памяти.
В перспективе, вероятно, будет принят единый стандарт кодирования текста, полностью учитывающий разнообразие существующих письменностей, на который постепенно перейдут все компьютеры, независимо от локации и используемого программного обеспечения. Но произойдет это, судя по всему, не скоро.
Кодирование изображений в двоичный код
Чтобы сохранить в двоичном коде фотографию, ее сначала виртуально разделяю на множество мелких цветных точек, называемых пикселями (что-то на подобии мозаики).
После разбивки на точки цвет каждого пикселя кодируется в бинарный код и записывается на запоминающем устройстве.
Если говорят, что размер изображения составляет, например, 512 х 512 точек, это значит, что оно представляет собой матрицу, сформированную из 262144 пикселей (количество пикселей по вертикали, умноженное на количество пикселей по горизонтали).
Прибором, «разбивающим» изображения на пиксели, является любая современная фотокамера (в том числе веб-камера, камера телефона) или сканер.
Чем на большее количество пикселей разделено изображение, тем реалистичнее выглядит фотография в декодированном виде (на мониторе или после распечатывания).
Однако качество кодирования фотографий в бинарный код зависит не только от количества пикселей, но также и от их цветового разнообразия.
Алгоритмов записи цвета в двоичном коде существует несколько. Самым распространенным из них является RGB. Эта аббревиатура – первые буквы названий трех основных цветов: красного – англ.Red, зеленого – англ. Green, синего – англ. Blue.
Из школьных уроков рисования, Вам, наверное, известно, что смешивая эти три цвета в разных пропорциях, можно получить любой другой цвет или оттенок.
На этом и построен алгоритм RGB. Каждый пиксель записывается в двоичном коде путем указания количества красного, зеленого и синего цвета, участвующего в его формировании.
Чем больше битов выделяется для кодирования пикселя, тем больше вариантов смешивания этих трех каналов можно использовать и тем значительнее будет цветовая насыщенность изображения.
Цветовое разнообразие пикселей, из которых состоит изображение, называется глубиной цвета.
Если для кодирования каждого пикселя какого-то изображения выделяется 8 битов двоичного кода, цветовое разнообразие составит 256 цветов.
Тем не менее, часто встречается и так называемая 32-битная глубина цвета. Она не предусматривает увеличение количества оттенков. Дополнительные биты, выделяемые для кодирования каждого пикселя, предназначены для регулирования степени его прозрачности или же не используются.
Описанная выше техника формирования изображений из мелких точек является наиболее распространенной и называется растровой. Но кроме растровой графики, в компьютерах используется еще и так называемая векторная графика.
Векторные изображения создаются только при помощи компьютера (фотокамеры этого делать «не умеют») и формируются не из пикселей, а из графических примитивов (линий, многоугольников, окружностей и др.).
Зачем нужна векторная графика? В известной детской песенке поется, что для изображения «человечка» достаточно нарисовать всего две «палки» и «огуречек». А представьте, насколько трудно вручную составить человечка из большого числа точек.
Векторное изображение в двоичном коде записывается как совокупность примитивов с указанием их размеров, цвета заливки, места расположения на холсте и некоторых других свойств.
Например, чтобы записать на запоминающем устройстве векторное изображение круга, компьютеру достаточно в двоичный код закодировать тип объекта (окружность), координаты его центра на холсте, длину радиуса, толщину и цвет линии, цвет заливки.
В растровой системе пришлось бы кодировать цвет каждого пикселя. И если размер изображения большой, для его хранения понадобилось бы значительно больше места на запоминающем устройстве.
Тем не менее, векторный способ кодирования не позволяет записывать в двоичном коде реалистичные фото. Поэтому все фотокамеры работают только по принципу растровой графики. Рядовому пользователю иметь дело с векторной графикой в повседневной жизни приходится не часто.
Кодирование звуковой информации
Любой звук, слышимый человеком, является колебанием воздуха, которое характеризируется двумя основными показателями: частотой и амплитудой.
Если графически изобразить звуковую волну, она будет выглядеть следующим образом:
Схему работы компьютера со звуком в общих чертах можно описать так.
Микрофон превращает колебания воздуха в аналогичные по характеристикам электрические колебания.
Динамики акустической системы или наушников имеют противоположное микрофону действие. Они превращают электрические колебания в колебания воздуха.
Но каким же образом звуковая карта преобразовывает электрические колебания в двоичный код?
Если взглянуть на графическое изображение волны и внимательно проанализировать ее геометрию, можно увидеть, что в каждый конкретный момент времени звук имеет определенную интенсивность (степень отклонения от начального состояния).
Значит если весь отрезок времени, в течение которого длится звук, разделить на очень маленькие временные участки, то звуковую волну можно будет записать как очередность значений интенсивности звука в каждом таком временном участке.
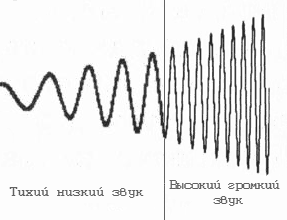
Но частота «дробления» звука должна быть достаточно высокой, иначе значения участков не будут отображать реальную геометрию волны. Вот примеры слишком низкой частоты дробления.
Описанный принцип разделения звуковой волны на мелкие участки и лежит в основе двоичного кодирования звука.
Аудиокарта компьютера разделяет звук на очень мелкие временные участки и кодирует степень интенсивности каждого из них в двоичный код. Такое «дробление» звука на части называется дискретизацией. Чем выше частота дискретизации, тем точнее фиксируется геометрия звуковой волны и тем качественней получается запись.
Так, простая речь (например, диктофонная запись) нормально воспринимается человеком, если частота дискретизации при кодировании была не ниже 8000 Гц (8 КГц). То есть, каждая секунда такой записи в двоичном коде должна состоять как минимум из 8000 частей.
Музыкальные же произведения, хранимые в компьютере, должны иметь еще более высокую частоту дискретизации. При записи стандартных звуковых CD она составляет минимум 44,1 КГц (44100 Гц).
Качество записи сильно зависит также от количества битов, используемых компьютером для кодирования каждого участка звука, полученного в результате дискретизации.
Представим, например, что для кодирования каждого такого участка компьютер использует 8 битов. Как известно, 8-битная ячейка может принимать одно из 256 значений. Но вдруг разнообразие интенсивности участков, полученных при дискретизации какого-то звука, оказалось более широким (например, 512 вариантов). В таком случае, компьютер «округлит» интенсивность участков до ближайших доступных значений чтобы «уложиться» в 256 вариантов и качество записи получится низким.
Количество битов, используемых для кодирования каждого участка звука, полученного при дискретизации, называется глубиной звука.
Глубины звука в 8-битов достаточно для кодирования простой речи. Но музыкальные произведения с такой глубиной будут звучать отвратительно. Поэтому гораздо чаще встречаются звуковые файлы, закодированные с глубиной 16, 24 или даже 32 бита.
Следует учитывать, что далеко не все устройства, предназначенные для воспроизведения «цифрового» звука, могут работать с файлами, закодированными с высокой частотой дискретизации и/или большой глубиной звука. Такие файлы могут проигрываться на одном компьютере, и «не открываться» на другом (если звуковая карта не поддерживает настолько высокий уровень дискретизации или глубины звука).
Особенности бинарного кодирования видео
Видеозапись состоит из двух компонентов: звукового и графического.
Кодирование звуковой дорожки видеофайла в двоичный код осуществляется по тем же алгоритмам, что и кодирование обычных звуковых данных (см. предыдущий пункт).
Принципы кодирования видеоизображения схожи с кодированием растровой графики (рассмотрено выше), хотя и имеют некоторые особенности.
Учитывая эту особенность, алгоритмы кодирования видео, как правило, предусматривают запись лишь первого (базового) кадра. Каждый же последующий кадр формируются путем записи его отличий от предыдущего.