Предикат что это такое
Предикат
Полезное
Смотреть что такое «Предикат» в других словарях:
ПРЕДИКАТ — (от лат. praedicatum сказанное) языковое выражение, обозначающее к. л. свойство или отношение. П., указывающий на свойство отдельного предмета (напр., «зеленый», «теплый»), называется одноместным. П., обозначающий отношение, называется… … Философская энциклопедия
ПРЕДИКАТ — (лат.). Сказуемое в предложении; то, что говорится о предмете. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРЕДИКАТ 1) сказуемое; 2) титул, почетное звание. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка
предикат — свойство, отношение, сказуемое Словарь русских синонимов. предикат сущ. • сказуемое Словарь русских синонимов. Контекст 5.0 Информатик. 2012 … Словарь синонимов
предикат — а, м. prédicat m. сказуемое. един. Титул после имени венценосной особы. Король в своеручной грамоте после отъезда маркиза Лопиталя неоднократно ея Величеству предикат Императорский писал. О сей ошибке в титулятуре не оставлено будет здесь и у вас … Исторический словарь галлицизмов русского языка
Предикат — (лат.). То же, что̀ сказуемое. Литературная энциклопедия: Словарь литературных терминов: В 2 х т. / Под редакцией Н. Бродского, А. Лаврецкого, Э. Лунина, В. Львова Рогачевского, М. Розанова, В. Чешихина Ветринского. М.; Л.: Изд во Л. Д. Френкель … Литературная энциклопедия
предикат — Лингвистический объект, аналогичный глаголу, сообщающий что либо о сущностях, обозначенных термами. [ГОСТ 34.320 96] предикат Функция, возвращающая логическое значение. [http://www.morepc.ru/dict/] Тематики базы данныхинформационные технологии в… … Справочник технического переводчика
ПРЕДИКАТ — в грамматике сказуемое … Большой Энциклопедический словарь
ПРЕДИКАТ — (от лат. praedicatum сказуемое) в узком смысле то же, что свойство; в широком смысле отношение, т. е. свойство нескольких предметов. В логике пропозициональная функция, т. е. выражение с неопределенными терминами (переменными), при выборе… … Большой Энциклопедический словарь
ПРЕДИКАТ — ПРЕДИКАТ, предиката, муж. (лат. praedicatum сказуемое) (научн.). 1. В логике понятие, определяющее предмет суждения субъект и раскрывающее его содержание (филос.). 2. То же, что сказуемое (грам.). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЕДИКАТ — ПРЕДИКАТ, а, муж. 1. В логике: понятие, определяющее предмет суждения (субъект). 2. В грамматике: член предложения, обозначающий отнесённый ко времени признак (действие или состояние). | прил. предикатный, ая, ое и предикативный, ая, ое (ко 2… … Толковый словарь Ожегова
Предикат — ПРЕДИКАТ (лат.). То же, что̀ сказуемое … Словарь литературных терминов
Что такое предикат: определение и примеры
Что такое предикат? Это слово встречается в лингвистике, математике, философии и программировании. Но не может же быть так, что в этих столь разных науках это слово имеет одинаковое значение? Математическая логика дает свою, особую трактовку этого термина. Начнем с нее.
Предикат в математике
В математической логике предикат обычно понимается как функция P: X → <правда, ложь>, называемая предикатом X. Однако предикаты имеют много разных применений и интерпретаций в математике и логике, и их точное определение, смысл и использование будут варьироваться от теории к теории. Так, например, если теория определяет понятие отношения, то предикат является просто характеристической функцией, иначе известной как индикаторная функция отношения. Однако не все теории имеют отношения или основаны на теории множеств, поэтому нужно быть осторожным с правильным определением и семантической интерпретацией предиката.
Правда или ложь
Свойства объектов
Предикаты в математической логике также широко используются, чтобы говорить о свойствах объектов, определяя набор всех объектов, имеющих общее свойство. Так, например, когда P является предикатом X, иногда можно сказать, что P является свойством X. Аналогично, обозначение P (x) используется для обозначения предложения или утверждения P относительно объекта переменной Х. Множество, определенное P (x), записывается как
Простым видом предиката (П) является булево выражение, и в этом случае входы в выражение сами являются значениями, объединенными с использованием булевых операций. Булево выражение со множеством истинности предиката является более сложным явлением.
Формальное определение
Предикат в грамматике
Существует два конкурирующих понятия предиката в теориях грамматики. Конкуренция между этими двумя концепциями породила путаницу в отношении использования термина «предикат» в теориях грамматики. Так что такое предикат? В этой статье рассматриваются оба эти понятия.
Первое понятие относится к традиционной грамматике, которая имеет тенденцию рассматривать предикат как одну из двух основных частей предложения, другая часть является предметом. Цель предиката состоит в том, чтобы завершить представление о предмете, например, что он делает или что из себя представляет.
Второе понятие было получено из работы в исчислении предикатов (логика предикатов, логика первого порядка) и является заметным в современных теориях синтаксиса и грамматики. В этом подходе предикат предложения в основном соответствует главному глаголу и любым вспомогательным средствам, которые сопровождают главный глагол. В то же время его аргументы (например, фразы существительные) находятся за пределами предиката.
В традиционной грамматике
Понятие П в традиционной грамматике вдохновлено пропозициональной логикой древности (в отличие от более современной логики предикатов). Предикат рассматривается как свойство, которое субъект имеет. Следовательно, предикат является выражением, которое может быть истинным. Таким образом, выражение «движется» верно для всего, что движется. Это дает ответ на вопрос, что такое предикат.
Такое классическое понимание предикатов было принято более или менее непосредственно в латинской и греческой грамматиках, и оттуда оно попало в грамматику английского и русского языков, где применяется непосредственно к анализу структуры предложения. Это понимание П также используется в англоязычных словарях.
Субъект и предикат
В синтаксисе
Синтаксический П указывает синтаксическую обоснованность применения произведения в формальной грамматике и аналогичен семантическому предикату, который определяет семантическую действительность применения произведения. В своей первоначальной реализации синтаксические предикаты имели форму «(α)?» и могли появляться только на левом краю произведения. Необходимым синтаксическим условием α может быть любой допустимый контекстно-свободный фрагмент грамматики.
Более формально синтаксический предикат представляет собой форму производственного пересечения, используемого в спецификациях парсера или в формальных грамматиках. В этом смысле термин имеет значение математической функции индикатора. Если p1 и p2 являются производственными правилами, язык, сгенерированный как p1, так и p2, является их заданным пересечением.
Размышляющие грамматики выражений (PEGs), изобретенные Брайаном Фордом, расширяют эти простые П, позволяя им появляться где угодно в пределах производства наравне с «не предикатами». Более того, Форд изобрел процедуру разбора для обработки этих грамматик в линейном времени.
Этот подход реализуется в ANTLR версии 3, которая использует детерминированные конечные автоматы для просмотра. Это может потребовать тестирования предиката для выбора между синтаксическими переходами (так называемый «пред-LL (*)» синтаксический анализ).
В современных теориях синтаксиса
Большинство современных теорий синтаксиса и грамматики берут свое начало в теории исчисления предикатов, связанных с Готлобом Фреге. Это понимание видит предикаты как отношения или функции, стоящие над аргументами. Они служат либо для назначения свойства одному аргументу, либо для связи двух или более аргументов друг с другом. Предложения состоят из предикатов и их аргументов (и дополнений) и являются, таким образом, структурами предикатного аргумента. В соответствии с ними данный П рассматривается как связывание его аргументов с большей структурой.
В логике
Логика первого порядка, также известная как исчисление предикатов первого порядка и логика предикатов, представляет собой набор формальных систем, используемых в математике, философии, лингвистике и информатике. Логика первого порядка использует квантованные переменные над объектами и позволяет использовать предложения, содержащие переменные. Это отличает его от логики высказываний, которая не использует кванторы или отношения.
Логика первого порядка
Подобные теории, как правило, является частью логики первого порядка вместе с определенной областью дискурса, по которой варьируются квантифицированные переменные. Иногда теория понимается в более формальном смысле, а это всего лишь набор предложений в логике первого порядка.
Используемые прилагательные отличают логику первого порядка от логики высших порядков, в которой есть П, имеющие определяющие предикаты или функции в качестве аргументов, или в которых разрешены один или оба квантора предикатов или кванторы функций. В теориях первого порядка предикаты часто связаны с множествами. В интерпретируемых теориях более высокого порядка их можно интерпретировать как множества. Нечто похожее используется и в определении предиката в программировании. Это не удивительно, ведь математика стала своего рода сырьем для этой науки.
Теоретическая часть
Существует много дедуктивных систем для видов суждений и логики первого порядка, которые являются как звуковыми (все доказуемые утверждения верны во всех моделях), так и полными (утверждения, которые верны для всех моделей, являются доказуемыми). Хотя отношение логического следствия разрешимо лишь наполовину, в автоматизированной теореме, доказанной в логике первого порядка, достигнут значительный прогресс. Логика первого порядка также удовлетворяет нескольким металогическим теоремам, которые делают ее пригодной для анализа в теории доказательств, такой как теорема Левенхайма-Сколема и теорема о компактности.
Логика первого порядка является стандартом для формализации математики в аксиомах и изучается в основах математики. Арифметика Пеано и теория множеств Цермело-Френкеля являются аксиоматизациями теории чисел и теории множеств, соответственно, являются частью логики первого порядка. Однако теория первого порядка не имеет возможности однозначно описывать структуру с бесконечной областью, например натуральные числа. Системы аксиом, которые полностью описывают эти две структуры (то есть системы категориальной аксиомы), могут быть получены в более сильных формах логики, таких как логика второго порядка.
Основы логики первого порядка были разработаны независимо Готлобом Фреге и Чарльзом Сандерсом Пирсом.
Предикат
Содержание
Определение
Предика́т (n-местный, или n-арный) — это функция с множеством значений 
(или «ложь» и «истина»), определённая на множестве 
. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».
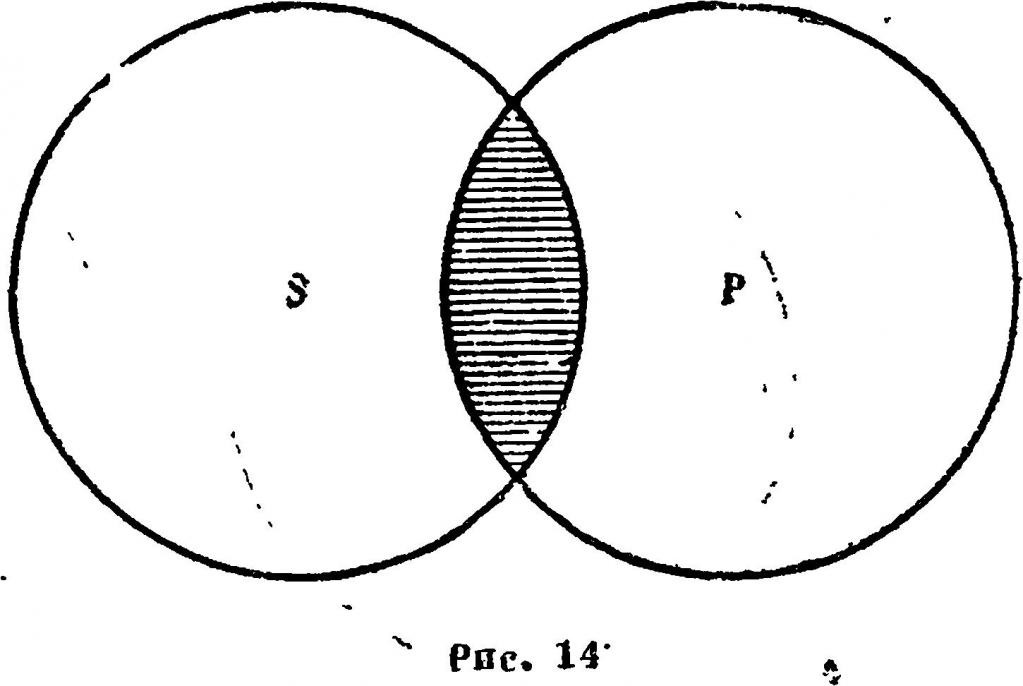
Предикат можно связать с математическим отношением: если (m1,m2. mn) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.
Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.
Предикат называют тождественно-истинным и пишут:
если на любом наборе аргументов он принимает значение 1.
Предикат называют тождественно-ложным и пишут:
если на любом наборе аргументов он принимает значение 0.
Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.
Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д
Примеры
Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y.
Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y», где множество M — это множество всех людей.
Предикат — это то, что утверждается или отрицается о субъекте суждения.
Операции над предикатами
Предикаты, так же, как высказывания, принимают два значения истинное и ложное, поэтому к ним применимы все операции логики высказываний. Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.
Логические операции
Конъюнкцией двух предикатов А(х) и В(х) называется новый предикат 
, который принимает значение «истина» при тех и только тех значениях х Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката А(х) В(х), х Х является пересечение множеств истинности предикатов А(х) – Т1 и В(х) – Т2, т.е. Т= Т1 ∩Т2. Например: А(х): «х – четное число», В(х): « х кратно 3». А(х) В(х) – «х – четное число и х кратно 3». Т.е. предикат «х делится на 6».
Дизъюнкцией двух предикатов А(х) и В(х) называется новый предикат 
, который принимает значение «ложь» при тех и только тех значениях х Т, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях. Областью истинности предиката А(х) В(х) является объединение областей истинности предикатов А(х) В(х).
Импликацией предикатов А(х) и В(х) называется новый предикат А(х) В(х), который является ложным при тех и только тех значениях х Т, при которых А(х) принимает значение «истина», а В(х) – значение «ложь» и принимает значение «истина» во всех остальных случаях. Читают: «Если А(х), то В(х)». Например. А(х): «Натуральное число х делится на 3». В(х): «Натуральное число х делится на 4», можно составить предикат: «Если натуральное число х делится на 3, то оно делится и на 4». Множеством истинности предиката А(х) В(х) является объединение множества Т2 – истинности предиката В(х) и дополнения к множеству Т1 истинности предиката А(х).
Кванторные операции
Квантор (все-)общности 
Квантор существования 
Квантор существования по переменной 
1
Предикат
Что такое предикат
Предикат (с латинского praedicatum означает «заявленное, упомянутое, сказанное») — понятие в логике, которым называют утверждение, высказанное о том или ином субъекте. Субъект высказывания — это та вещь или явление, о котором или которой делается утверждение.
Одна из важнейших особенности логики предикатов в том, что все общие имена (такие, как «цветок», «деревня»), знаки свойств («розовый», «большая») и знаки отношений («красивее», «роднее») рассматриваются как относящиеся к одной категории знаков: категории предикаторов (иначе говоря, предметно-истинных функторов).
Предикаторы, в свою очередь, показывают функции, у которых вероятные аргументы — это универсальные в рассмотрении объекты, а значения — истинные оценки. В классической логике они называются «истина» и «ложь». К примеру, возьмем предикатор «человек», который представляет функцию, определяемую как истина каждым отдельным человеком, а каждым отличным от человека существом — как ложь.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Другой пример : функция, которая соответствует предикатору «больше», сопоставляет истину каждой паре объектов или субъектов, один из которых больше. Например, такая пара, как «слон, мышь». Но всем остальным парам, по типу «мышь, слон» и «мышь, мышь», такая функци будет сопоставлять оценку «ложь».
Предикаторы могут быть:
Логические операции над предикатами
Так как предикаты принимают два значения, «истина» и «ложь» (1 и 0), к ним можно применить все операции алгебры логики.
Представим, что в неком множестве N определены два предиката P(x) и Q(x). Рассмотрим все операции с ними по-отдельности.
Область истины в этом случае — объединение областей истинности обоих утверждений.
Область истины здесь — дополнение множества истинности утверждения P(x) до множества N, иначе говоря \(I_overline
=N\I_P=CI_P.\)
Кванторные операции над предикатами
Прежде чем изучить квантовые операции, нужно разобраться, что из себя представляет сам квантор.
Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание.
Кванторы впервые были определены немецким математиком Готлобом Фреге. Он упомянул их в своей работе «Begriffsschrift» («Исчисление понятий», 1879 года). Однако сам термин был изобретен английским логиком Чарльзом Пирсом в 1885 году. Вместе со словом «квантор» он ввел также и термин «квантификация», который означает измерение качеств признаков.
Обозначение кванторов
Символическое обозначение кванторов придумал итальянский математик Дж. Пеано в 90-е годы XIX века. Выглядят эти символы так:
\(\forall\) — «для любого», «для каждого», «для всех»;
\(\exists\) — «существует», «найдётся».
! – «единственный»;
: – «такой, что»;
| – «такой, что».
Знак «:» обычно используется в формулировках определений или теорем, которые записываются с помощью кванторов. Знак «|» применяется в определениях множеств.
Виды кванторов
Квантор общности \(\forall\)
Оно истинно только в том случае, когда \(P(x)\) — тождественно истинен. В ином случае данное высказывание ложно.
Оно истинно только в том случае, когда одноместный предикат \(P(x, a_2, …, a_n)\) на множестве \(N_1\) тождественно истинен. В противном случае оно ложно.
Квантор существования \( \exists\)
Примеры применения
Использование предикатов
Использование кванторов
Пусть предикат «x кратно 5». Тогда с помощью квантора общности можно записать ложные высказывания:
В этом случае решение будет выглядеть так:
Чтобы обозначить истинные высказывания, используем квантор существования:
В записи оно будет выглядеть так:
На множестве x простых чисел существует предикат: «Простое число является нечетным». Если мы поставим перед предикатом слово «любое», то получим ложное высказывание «Любое простое число является нечетным». Если мы поставим перед предикатом слово «существует», то получим истинное высказывание «Существует простое число, которое является нечетным».
Так, предикат можно превратить в высказывание, если поставить перед ним квантор.
Предикат (лингвистика)
В западно-европейской терминологии лингвистики (напр., англ. predicate и др.) используется не только в значении «предикат», но и в значении «сказуемое». В других языках, в том числе и русском, термин praedicatum был заменён калькой «сказуемое», таким образом логическая и грамматическая категории оказались разделены. То есть, «сказуемое» ассоциируется с формальной стороной (член предложения), а «предикат» — с содержательной, семантической стороной.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Глагольной группой (ГГ, англ. Verb phrase, VP) в лингвистике называют синтаксическую единицу, состоящую из по меньшей мере одного глагола и его зависимых, таких как дополнения, комплементы и другие модификаторы. Исключение составляет подлежащее, не входящее в состав глагольной группы. Так, в предложении Толстый мужчина быстро положил бриллианты в коробку слова быстро положил бриллианты в коробку могут считаться глагольной группой, состоящей из глагола положил и его зависимых, но не включающей в себя.
Активный язык (фиентивный строй, активная типология, активность; лат. activus — деятельный, действенный) — язык, обладающий типологией, ориентированной на семантическое противопоставление не субъекта и объекта, как в языках номинативного строя, а так называемого активного и инактивного начал.
В лингвистике хабитуáлис, или хабитуальный аспект, — это набор грамматических или лексических значений, выражающих регулярное повторение действия или привычность, традиционность состояния. Хабитуальный аспект можно считать частным случаем имперфектива, и тогда он противопоставляется второй разновидности имперфектива — дуративу.