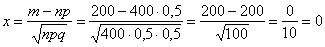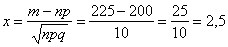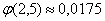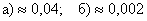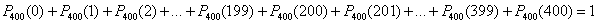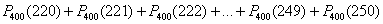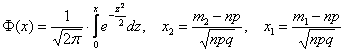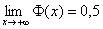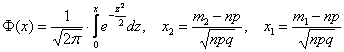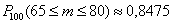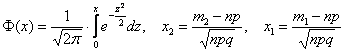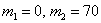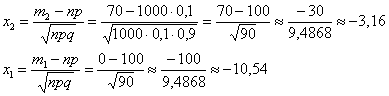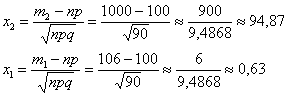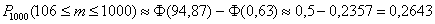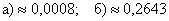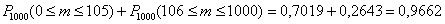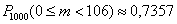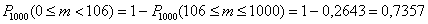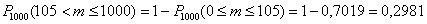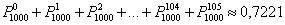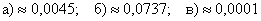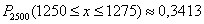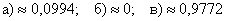Предел лапласа чему равен
Локальная и интегральная теоремы Лапласа
Данная статья является естественным продолжением урока о независимых испытаниях, на котором мы познакомились с формулой Бернулли и отработали типовые примеры по теме. Локальная и интегральная теоремы Лапласа (Муавра-Лапласа) решают аналогичную задачу с тем отличием, что они применимы к достаточно большому количеству независимых испытаний. Не нужно тушеваться слов «локальная», «интегральная», «теоремы» – материал осваивается с той же лёгкостью, с какой Лаплас потрепал кучерявую голову Наполеона. Поэтому безо всяких комплексов и предварительных замечаний сразу же рассмотрим демонстрационный пример:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет 200 раз.
По характерным признакам здесь следует применить формулу Бернулли 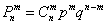
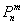
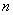
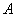
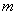
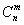
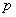
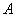
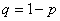
Применительно к нашей задаче:
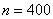
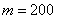
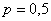
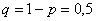
Таким образом, вероятность того, что в результате 400 бросков монеты орёл выпадет ровно 200 раз: 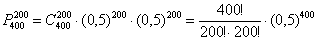
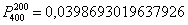
Заостряю ваше внимание, что получено точное значение и такое решение вроде бы идеально. На первый взгляд. Перечислим веские контраргументы:
– во-первых, программного обеспечения может не оказаться под рукой;
– и во-вторых, решение будет смотреться нестандартно (с немалой вероятностью придётся перерешивать);
Поэтому, уважаемые читатели, в ближайшем будущем нас ждёт:
Локальная теорема Лапласа
Если вероятность 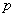
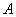
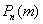
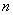
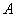
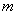
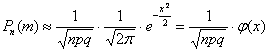
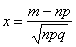
При этом, чем больше 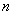
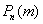
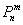
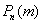
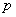
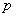
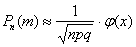
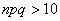
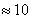
Так, например, если 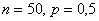
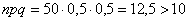
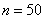
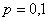
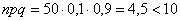
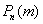
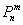
О том, почему 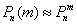
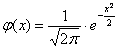
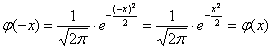
Оформим официальные отношения с нашим примером:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно:
а) 200 раз;
б) 225 раз.
С чего начать решение? Сначала распишем известные величины, чтобы они были перед глазами:
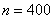
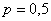
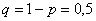
а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно 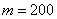
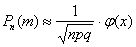
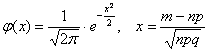
На первом шаге вычислим требуемое значение аргумента:
Далее находим соответствующее значение функции: 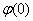
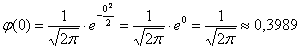
Округление проводят, как правило, до 4 знаков после запятой.
Недостаток прямого вычисления состоит в том, что экспоненту переваривает далеко не каждый микрокалькулятор, кроме того, расчёты не особо приятны и отнимают время. Зачем так мучиться? Используйте калькулятор по терверу (пункт 4) и получайте значения 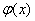
Кроме того, существует таблица значений функции 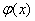
На заключительном этапе применим формулу 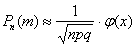
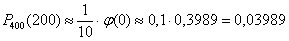
Как видите, полученный результат очень близок к точному значению 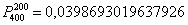
б) Найдём вероятность того, что в серии из 400 испытаний орёл выпадет ровно 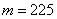
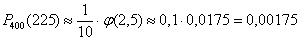
Ответ:
Следующий пример, как многие догадались, посвящён деторождению – и это вам для самостоятельного решения 🙂
Вероятность рождения мальчика равна 0,52. Найти вероятность того, что среди 100 новорожденных окажется ровно: а) 40 мальчиков, б) 50 мальчиков, в) 30 девочек.
Результаты округлить до 4 знаков после запятой.
…Интересно тут звучит словосочетание «независимые испытания» =) Кстати, реальная статистическая вероятность рождения мальчика во многих регионах мира колеблется в пределах от 0,51 до 0,52.
Примерный образец оформления задачи в конце урока.
Все заметили, что числа получаются достаточно малыми, и это не должно вводить в заблуждение – ведь речь идёт о вероятностях отдельно взятых, локальных значениях (отсюда и название теоремы). А таковых значений много, и, образно говоря, вероятности «должно хватить на всех». Правда, многие события будут практически невозможными.
Поясню вышесказанное на примере с монетами: в серии из четырёхсот испытаний орёл теоретически может выпасть от 0 до 400 раз, и данные события образуют полную группу:
Однако бОльшая часть этих значений представляет собой сущий мизер, так, например, вероятность того, что орёл выпадет 250 раз – уже одна десятимиллионная: 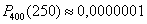
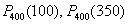
С другой стороны, не следует недооценивать и скромные результаты: если 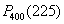
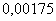
А теперь задумаемся: как вычислить данную вероятность? Не считать же по теореме сложения вероятностей несовместных событий сумму:
Гораздо проще эти значения объединить. А объединение чего-либо, как вы знаете, называется интегрированием:
Интегральная теорема Лапласа
Если вероятность 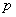
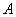
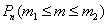
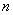
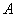
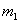
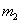
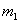
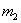
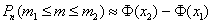
При этом количество испытаний, разумеется, тоже должно быть достаточно большим и вероятность 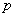
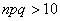
Функция 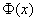
На практике наиболее часто встречаются следующие значения:
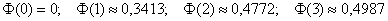
Начиная с 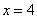
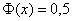
Кроме того, функция Лапласа нечётна: 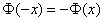
Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Я подобрал наиболее реалистичный пример, а то у меня тут нашлось несколько задач, в которых стрелок делает тысячи выстрелов =)
Решение: в данной задаче речь идёт о повторных независимых испытаниях, причём их количество достаточно велико. По условию требуется найти вероятность того, что мишень будет поражена не менее 65, но и не более 80 раз, а значит, нужно использовать интегральную теорему Лапласа: 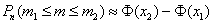
Для удобства перепишем исходные данные в столбик:
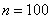
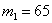
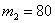
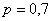
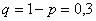
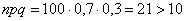
Вычислим значения аргументов: 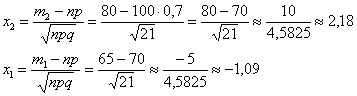
Обращаю ваше внимание, что произведение 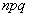
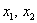
Используем указанную выше таблицу либо расчётный макет по терверу (пункт 5).
В качестве письменного комментария советую поставить следующую фразу: значения функции 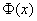
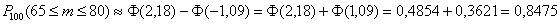
– вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Обязательно пользуемся нечётностью функции! На всякий случай распишу подробно: 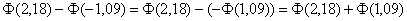
Дело в том, что таблица значений функции 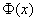
Ответ:
Результат чаще всего округляют до 4 знаков после запятой (опять же в соответствии с форматом таблицы).
Для самостоятельного решения:
В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет включено не менее 1250 и не более 1275 ламп.
Примерный образец чистового оформления в конце урока.
Следует отметить, что рассматриваемые задачи очень часто встречаются в «обезличенном» виде, например:
Производится некоторый опыт, в котором случайное событие 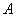
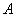
И подобных формулировок выше крыши. По причине трафаретности задач условие нередко стремятся завуалировать – это «единственный шанс» хоть как-то разнообразить и усложнить решение:
В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую на большой перемене с вероятностью 0,1. Какова вероятность того, что в обычный учебный день:
а) столовая будет заполнена не более чем на две трети;
б) посадочных мест на всех не хватит.
Обращаю внимание на существенную оговорку «в ОБЫЧНЫЙ учебный день» – она обеспечивает относительную неизменность ситуации. После праздников в институт может прийти значительно меньше студентов, а на «День открытых дверей» нагрянуть голодная делегация =) То есть, в «необычный» день вероятности будут заметно отличаться.
Решение: используем интегральную теорему Лапласа 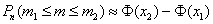
В данной задаче:
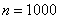
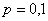
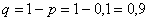
а) Вычислим, сколько посадочных мест составляют две трети от общего количества: 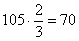
Найдём вероятность того, что в обычный учебный день столовая будет заполнена не более чем на две трети. Что это значит? Это значит, что на большой перемене придут от 0 до 70 человек. То, что никто не придёт или придут всего несколько студентов – есть события практически невозможные, однако в целях применения интегральной теоремы Лапласа эти вероятности все равно следует учесть. Таким образом:
Вычислим соответствующие аргументы:
В результате: 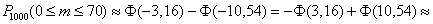
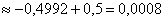
Напоминание: при 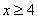
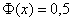
б) Событие «Посадочных мест на всех не хватит» состоит в том, что в столовую на большой перемене придут обедать от 106 до 1000 человек (главное, хорошо уплотнить =)). Понятно, что высокая посещаемость невероятна, но тем не менее: 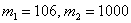
Рассчитываем аргументы:
Таким образом, вероятность того, что посадочных мест на всех не хватит:
Ответ:
А теперь остановимся на одном важном нюансе метода: когда мы проводим вычисления на отдельно взятом отрезке, то всё «безоблачно» – решайте по рассмотренному шаблону. Однако в случае рассмотрения полной группы событий следует проявить определённую аккуратность. Поясню этот момент на примере только что разобранной задачи. В пункте «бэ» мы нашли вероятность 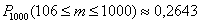
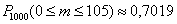
Поскольку эти события противоположны, то сумма вероятностей должна равняться единице:
?! В чём дело? – вроде бы тут всё логично. Дело в том, что функция Лапласа является непрерывной, а мы не учли интервал от 105 до 106. Вот здесь то и пропал кусочек 0,0338. Поэтому по той же самой стандартной формуле следует вычислить:
Ну, или ещё проще:
Возникает вопрос: а что, если мы СНАЧАЛА нашли 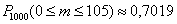
Но как так может быть?! – в двух способах получаются разные ответы! Всё просто: интегральная теорема Лапласа – это метод приближённого вычисления, и поэтому приемлемы оба пути.
Для более точных расчётов следует воспользоваться формулой Бернулли и, например, экселевской функцией БИНОМРАСП. В результате её применения получаем:
И я выражаю благодарность одному из посетителей сайта, который обратил внимание на эту тонкость – она выпала из моего поля зрения, так как исследование полной группы событий редко встречается на практике. Желающие могут ознакомиться с содержательной дискуссией по этому поводу.
Заключительный пример для самостоятельного решения:
В обычный учебный день вероятность присутствия студента на лекции равна 0,8. Найти вероятность того, что из 100 студентов на лекции будут присутствовать:
а) 85-90%;
б) половина студентов;
в) не менее 72 студентов.
Постарайтесь не пропускать задание 😉 Краткое решение и ответ совсем близко.
Здесь, несмотря на оговорку, все равно не всё гладко: известно, что процент прогулов у юношей заметно отличается от аналогичного показателя у девушек, поэтому усреднённая оценка несколько некорректна. Задачу следовало бы сформулировать для кадетского корпуса либо Института благородных девиц =) Неожиданно, но юноши, скорее всего, посещают занятия лучше =)
Вспомнилась, к слову, коварная задачка: вероятно ли встретить на улице 100 мужчин подряд? Запросто! Если навстречу прошагает рота солдат. Многие думают, что шансы встретить мужчину либо женщину составляют примерно 50 на 50 и даже встреча подряд десяти прохожих одного пола крайне маловероятна. Но почти все забывают об условии равновозможности событий. Так, например, если за углом находится отделение полиции или швейная фабрика, то встреча мужчины/женщины будет совсем не равновозможной.
Подобные моменты нужно обязательно учитывать в своих статистических исследованиях, которые бывают у каждого из нас хотя бы на бытовом уровне =)
Задача 2: Решение: по условию:
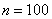
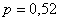
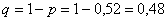
Используем локальную теорему Лапласа 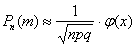
а) 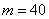
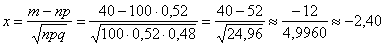
Примечание: «икс» обычно округляют до 2 знаков после запятой.
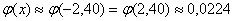
Примечание: на практике часто пользуются стандартной таблицей значений функции 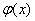
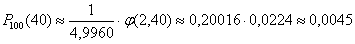
б) 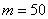
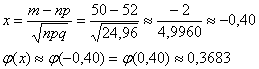
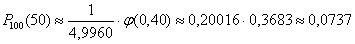
в) 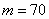
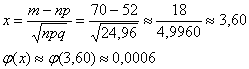
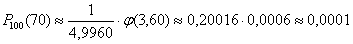
Ответ:
Задача 4: Решение: используем интегральную теорему Лапласа: 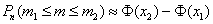
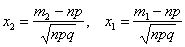
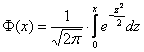
В данной задаче:
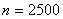
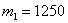
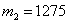
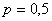
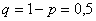
Вычислим аргументы: 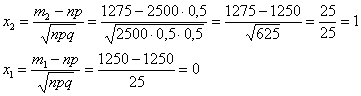
Значения функции 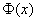
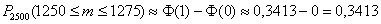
Ответ:
Задача 6: Решение: в данной задаче:
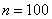
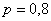
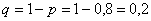
а) Найдём количество студентов, соответствующее 85 и 90 процентам: 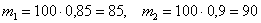
Для контроля дальнейших вычислений используйте полностью автоматизированную программу >>> Это бонус для самых терпеливых читателей!
Используем интегральную теорему Лапласа: 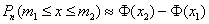
В данном случае: 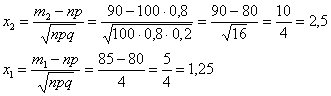
Таким образом:
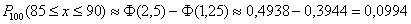
б) Используем локальную теорему Лапласа: 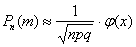
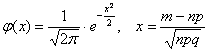
В данном случае 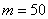
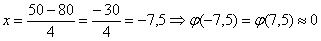
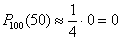
в) Используем интегральную теорему Лапласа: 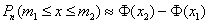
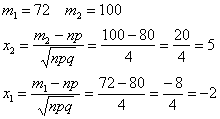
В результате: 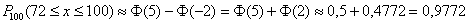
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)