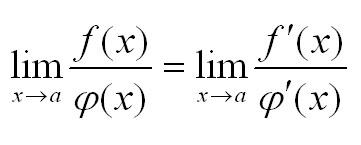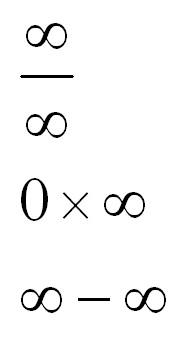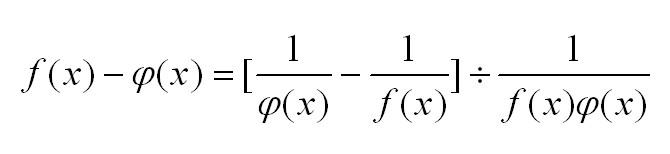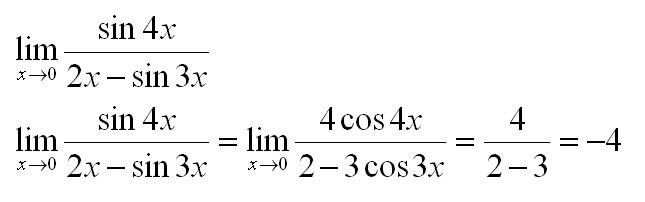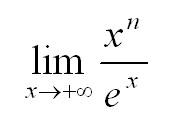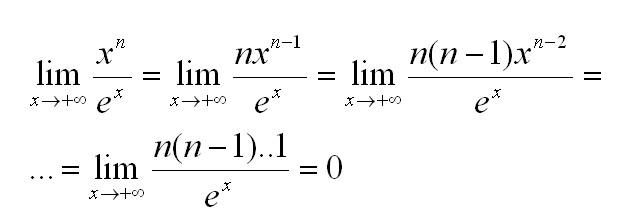Правило лопиталя это что

Правило Лопиталя для чайников: определение, примеры решения, формулы

Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.

Правило Лопиталя: история и определение

На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.

Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.

Пределы

Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.

Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.

Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:

Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:

Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Раскрытие неопределенностей по правилу Лопиталя

В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:

Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.

Неопределенности

Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:

Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:

Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:

Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:

Таблица производных

Теперь перейдем к примерам.

Пример 1

Найти предел по правилу Лопиталя:

Пример 2

Вычислить с использованием правила Лопиталя:

Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.

Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:

Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

В чем заключается правило Лопиталя?

Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.

Правило Лопиталя: история и определение

Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя.

Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности.

Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места. Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:

Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:

Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.

Раскрытие неопределенностей по правилу Лопиталя

В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:

Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.

Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:

Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:

Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:

Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:

Пример 1

Найти предел по правилу Лопиталя:

Пример 2

Вычислить с использованием правила Лопиталя:

Важный момент!
Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.

Решение пределов функций, используя правило Лопиталя

Изложен метод решения пределов, используя правило Лопиталя. Приводятся формулировки соответствующих теорем. Подробно разобраны примеры решения пределов, содержащих неопределенности ∞/∞, 0/0, 0 в степени 0 и ∞ – ∞, с помощью правила Лопиталя.

Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов функций является использование правила Лопиталя. Оно позволяет раскрывать неопределенности вида 0/0 или ∞/∞ в конечной или бесконечно удаленной точке, которую мы обозначим как x0.

Для применения этого правила, должна существовать такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и функция в знаменателе и ее производная не обращается в нуль.

Применение правила Лопиталя состоит из следующих шагов:

Правило Лопиталя. Формулировки теорем

Здесь мы приводим формулировки теорем, на которых основывается раскрытие неопределенностей по правилу Лопиталя.

Источник

Предел функции, правило Лопиталя

Самой важной частью правила Лопиталя является дифференцирование функции и нахождение ее производной.

Правило Лопиталя

Если неопределенность нерешаема после применения правила Лопиталя, тогда необходимо снова его применить. Для полного понятия рассмотрим несколько примеров.

Теперь можно переходить к вычислению пределов, используя правило. Получаем, что

Производим постановку бесконечностью. Получаем, что

lim x → ∞ ln ( x ) x = ln ( ∞ ) ∞ = » open=» ∞ ∞

Полученная неопределенность указывает на то, что необходимо применить правило Лопиталя. Имеем, что

lim x → ∞ ln ( x ) x = » open=» ∞ ∞ = lim x → ∞ ln ( x ) ‘ x ‘ = lim x → ∞ 1 x 1 = 1 ∞ = 0

Ответ: lim x → ∞ ln ( x ) x = 0

Вычислить предел заданной функции lim x → 0 + 0 ( x 4 ln ( x ) )

Решение привело к неопределенности вида ноль умноженный на отрицательную бесконечность. Это указывает на то, что необходимо обратиться к таблице неопределенностей и принять решения для выбора метода нахождения этого предела. После преобразования применяем правило Лопиталя. Получаем, что

Приход к неопределенности говорит о том, что необходимо повторное применение этого правила. Имеем, что

Ответ: lim x → 0 + 0 ( x 4 ln ( x ) ) = 0

После подстановки получаем

Наличие неопределенности указывает на то, что следует использовать правило Лопиталя. Получаем, что

Для последнего перехода использовался первый замечательный предел. После чего приходим к решению по Лопиталю. Получим, что

Так как неопределенность не ушла, необходимо еще одно применение правила Лопиталя. Получаем предел вида

Источник

Правило Лопиталя

Вы будете перенаправлены на Автор24

Правило Лопиталя

Правило Лопиталя было открыто шведским математиком Иоганном Бернулли, который затем рассказал в письме о нём Лопиталю. Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.

Правило Лопиталя применяется для выражений, сводимых к неопределенностям следующего вида:

Вместо нуля в первом выражении может быть какая-либо бесконечно малая величина.

В общем случае правилом Лопиталя можно воспользоваться, если и в числителе, и в знаменателе одновременно нуль или бесконечность.

Условия, при которых можно применять правило Лопиталя:

Доказательство правила Лопиталя:

Готовые работы на аналогичную тему

Алгоритм вычисления решения с использованием правила Лопиталя

Пример № 1:

Проверим условия применимости правила Лопиталя:

Запишем производную и найдем предел функции:

Пример № 2:

Проверим условия применимости правила Лопиталя:

Запишем производную и найдем предел функции:

Повторяем вычисление производной пока не избавимся от неопределенности:

Пример № 3:

Пример № 4:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 12 2021

Источник

Правило Лопиталя

При вычислении предела отношения \(\displaystyle \frac\) при \(x\rightarrow a\) в случае, когда функции \(f\) и \(g\) одновременно являются либо бесконечно малыми, либо бесконечно большими, иногда удобно применить так называемое правило Лопиталя, позволяющее заменять предел отношения функций пределом отношения их производных.

Неопределенность вида \(\displaystyle \frac<0><0>\).

\(\triangle\) Обозначим \(f(x)=3x^10-2x^5-1\), \(g(x)=x^3-4x^2+3\). Тогда \(f'(x)=30x^9-10x^4\), \(g'(x)=3x^2-8x\), \(f(1)=g(1)=0\), \(f'(1)=20\), \(g'(1)=-5\), и по формуле \eqref находим, что искомый предел равен \(-4\). \(\blacktriangle\)

\(\circ\) Пусть \(x\in(a,b)\). Доопределим функции \(f(x)\) и \(g(x)\) в точке \(a\), полагая
$$
f(a)=g(a)=0.\label
$$
Тогда из условий \eqref и \eqref следует, что функции \(f\) и \(g\) непрерывны на отрезке \([a,x]\). По теореме Коши существует точка \(\xi\in (a,x)\) такая, что
$$
\frac=\frac=\frac.\label
$$
Если \(x\rightarrow a+0\), то \(\xi\rightarrow a+0\) и в силу условия \eqref существует \(\displaystyle \lim_\frac=A\). Поэтому из равенства \eqref следует, что справедливо утверждение \eqref. \(\bullet\)

Доказанная теорема (с соответствующими изменениями ее условий) остается справедливой при \(x\rightarrow a-0\) и \(x\rightarrow a\), где \(a\) — конечная точка.

Эта теорема остается в силе и для случая, когда \(a=+\infty\) (или \(a=-\infty\)), если \(\displaystyle \lim_f(x)=\lim_ g(x)=0,\ g'(x)\neq 0\) при \(x > x_0\) и существует \(\displaystyle \lim_\frac=A\); в этом случае \(\displaystyle \lim_\frac=A\). Доказательство этого утверждения основано на использовании замены переменного \(\displaystyle x=\frac<1>\) и теоремы 1.

Неопределенность вида \(\displaystyle \frac<\infty><\infty>\).

\(\circ\) Из условий \eqref следует, что
$$
\exists\alpha_ <1>> \alpha:\ \forall x > \alpha_<1>\rightarrow\ |f(x)| > 1,\ |g(x)| > 1,\label
$$
и поэтому \(f(x)\neq 0,\ g(x)\neq 0\) при \(x > \alpha_1\). По определению предела \eqref для заданного числа \(\varepsilon > 0\) можно найти \(\delta=\delta_1(\varepsilon)\geq \alpha_1\) такое, что для всех \(t > \delta_<1>\) выполняется неравенство
$$
A-\frac<\varepsilon> <2> Рис. 19.1

Фиксируя \(x_ <0>> \delta_<1>\) (рис. 19.1), выберем, пользуясь условиями \eqref, число \(\delta_ <2>> x_<0>\) такое, чтобы при всех \(x > \delta_<2>\) выполнялись неравенства
$$
\left|\frac)>\right| \delta\) выполняется неравенство
$$
A-\varepsilon \delta\), применим к функциям \(f\) и \(g\) на отрезке \([x_0,x]\) теорему Коши о среднем. В силу этой теоремы существует точка \(\xi\in [x_<0>,x]\) такая, что
$$
\frac)>)>=\frac.\label
$$
Преобразуем левую часть равенства \eqref, используя условия \eqref и \eqref:
$$
\frac)>)>=\frac(\varphi(x))^<-1>,\label
$$
где
$$
\varphi(x)=\frac<1-g(x_0)/g(x)><1-f(x_0)/f(x)>=1+\beta(x).\label
$$
Заметим, что \(\beta(x)\rightarrow 0\) при \(x\rightarrow +\infty\) в силу условий \eqref. Поэтому
$$
\forall \varepsilon > 0\ \exists\delta\geq\delta_<2>:\ \forall x > \delta\rightarrow|\beta(x)| x_ <0>> \delta_<1>\), то из равенств \eqref, \eqref и условия \eqref следует, что для всех \(x > \delta_<2>\) выполняется неравенство
$$
A-\frac<\varepsilon> <2>\delta\), то \(\phi(x) > 0\) в силу условий \eqref и \eqref, и поэтому неравенство \eqref равносильно следующему:
$$
(A-\frac<\varepsilon><2>)(1+\beta(x)) A-\frac<\varepsilon><2>-\frac<\varepsilon><2>=A-\varepsilon.\nonumber
$$
Аналогично находим
$$
\left(A+\frac<\varepsilon><2>\right)(1+\beta(x)) \leq A+\frac<\varepsilon><2>+\left(|A|+\frac<\varepsilon><2>\right)|\beta(x)| \delta\) выполняется неравенство \eqref. это означает, что справедливо утверждение \eqref. \(\bullet\)

Теорема 2 остается в силе и в случае, когда \(A=+\infty\) или \(A=-\infty\). Теорема справедлива и для случая \(x\rightarrow a\ (x\rightarrow a-0,\ x\rightarrow a+0)\), где \(a\) — конечная точка.

Согласно теореме 1 и теореме 2 правило Лопиталя служит для раскрытия неопределенностей вида \(\displaystyle \frac<0><0>\) или \(\displaystyle \frac<\infty><\infty>\). Неопределенности видов \(0\cdot \infty,\ \infty-\infty,\ 0^<0>,\ \infty^<0>,\ 1^<\infty>\) часто удается свести к неопределенностям типа \(\displaystyle \frac<0><0>\) или \(\displaystyle \frac<\infty><\infty>\) с помощью различных преобразовании.

Источник