Правило что такое площадь 2 класс правило

Тема урока «Площадь фигуры. Единицы площади». 2-й класс

Класс: 2

Презентация к уроку

Цель: познакомиться с понятием площадь фигуры.

Оборудование: презентация, модели: квадратные сантиметры, квадратные дециметры, квадратные метры.

1. Организационный момент.Здравствуй, мой любимый класс,
Очень рада видеть вас!
Ты готов начать урок?
Всё ль на месте?
Всё ль в порядке?
Ручки, книжки и тетрадки?Приветствуют учителя.

Проверяют свою готовность к уроку.II. Актуализация знаний.

Устный счёт.1)Вставьте пропущенные числа.

В аллее 28 каштанов, а ясеней в 4 раза меньше. Сколько ясеней растёт в аллее?Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения.III. Определение темы урока.

2. Постановка проблемы.– Как называются данные на доске фигуры?

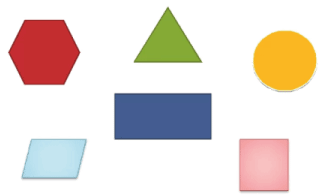
– Что их объединяет? (Это многоугольники, стороны которых равны 2 см.)

– Как найти периметр каждого многоугольника?

2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см).

2 + 2 + 2 + 2 + 2 = 10 (см).

– Как найти площадь этих фигур?

– Какие трудности у вас возникли?

– Сегодня на уроке мы узнаем, что называют площадью фигуры.

Фиксируют затруднение.IV. Открытие нового знания.Какая фигура меньше занимает места на плоскости?

Говорят, что треугольник имеет меньшую площадь, четырёхугольник.

— Площадь какой фигуры больше?

Площадь – свойство фигуры, занимать место на плоскости.

Площадь – это внутренняя часть фигуры.

— Площадь квадрата больше, чем площадь круга?

— Площадь какой фигуры больше красной или жёлтой?

— Сможем ли мы сравнить площади фигур наложением?

— Наложить мы не сможем эти фигуры, но можем разделить на квадраты и узнать, сколько квадратов занимают фигуры.

Площадь фигуры можно измерять и другими мерками.

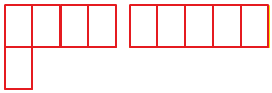
Сравните жёлтый и красный прямоугольники по количеству квадратов.

— Сколько квадратов в первом прямоугольнике, во втором?

— Почему так получилось?

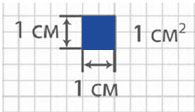
Чтобы этого не было вводятся специальные размеры квадратов. Длина стороны квадрата 1 см.Работают с презентацией.

Треугольник занимает меньше места.

Площадь четырёхугольника больше, чем площадь треугольника. Это видно на глаз.

Площадь квадрата больше, чем площадь круга. Проверим способом наложения.

Площадь двух кругов одинаковая.

Сравнивают прямоугольники по количеству квадратов.

Т.к. фигуры разбиты на квадраты разных размеров.V. Первичное закрепление.

Работа в парах.— Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь.

Фигуры у всех разные, но что у них одинаковое?

-Образуйте фигуры, площадь которой 5 кв. см. (4 кв.см) Назовите площадь.

Чтение правила по учебнику стр. 27.

(Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.)

– Сформулируйте определение квадратного метра.

– Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади.

– Сравните попарно площади этих квадратов.

Работают в парах. У учащихся модели 1кв. см.

У наших фигур одинаковые площади.

Читают определение квадратного дециметра, формулируют определение квадратного сантиметра, метра.

Сравнивают попарно площади этих квадратов, накладывая меньший квадрат на больший.Физминутка.Определите площади фигур на экране.

Работа в печатной тетради № 2.

Напиши площадь данных фигур.Читают величины, записанные единицами площади.

Записывают площадь фигур.VII. Итог урока.Выбери правильное утверждение:

1. Единицы измерения площади:
а) см
б) кв.см
в) кг

– Назовите единицы измерения площади фигуры.

Пригодится ли вам в жизни умение находить площадь фигур?

Выбирают правильное утверждение.Рефлексия деятельности.Покажите своё настроение в конце урока смайликом.

— Что не получилось? Почему?

Источник

Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

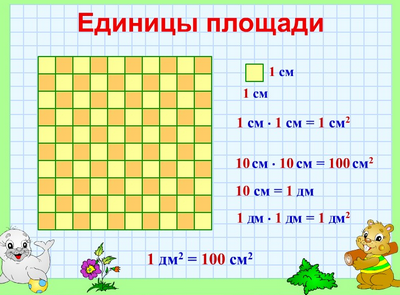
Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.

Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

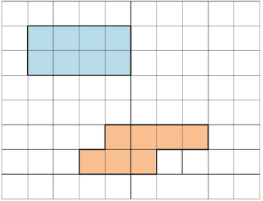
Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

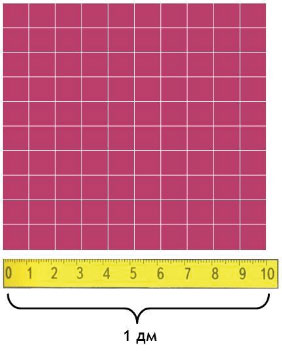
Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

Значит, 1 дм² = 100 см²

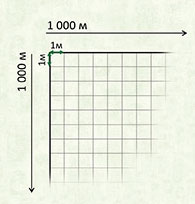
Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

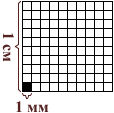
Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

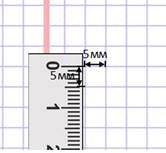
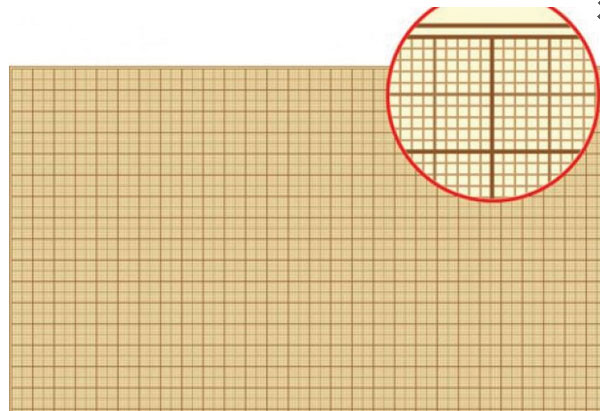
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Слово «ар» при числах сокращённо записывают так:

Гектар

Слово «гектар» при числах сокращённо записывают так:

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.

Поделись с друзьями в социальных сетях:

Источник

Конспект урока по математике по теме » Площадь», 2 класс

Открытый урок по математике во 2 классе

Тема: Площадь. Единицы площади.

Цели: 1.Сформировать понятия «площадь» и «единицы площади»; учить измерять площадь фигур заданными мерками;

2.Развивать логическое мышление, речь, память, внимание, математические и исследовательские способности;

3.Воспитывать умение работать в парах, группах; прививать любовь к изучению геометрии.

Тип урока: изучение нового материала (на основе учебной исследовательской деятельности)

репродуктивный (повторение изученных геометрических фигур, величин и мер их измерения);

словесный (информационные сообщения учителя, беседа, стихотворение);

наглядный (работа с таблицами и схемами);

практический ( вычерчивание геометрических фигур на основе программы действий, измерение площади прямоугольников разными мерами);

частично-поисковый (исключение «лишних» мер, определение темы урока);

исследовательский (выбор самой удобной меры для измерения площади,

исследование причин, по которым из прямоугольников с одинаковым Р площадь квадрата является наибольшей)

Оборудование: схема «Величина»; схема «Дерево понятий»; таблица «Программа действий»; сигнальные квадраты; карточки; конверты с набором мер разных геометрических форм; конверты с набором стандартных мер для измерения площади

Методы стимулирования и мотивации:

— стимулирование интереса к учению через организацию игры «Путешествие по стране Геометрии» и самооценку;

— стимулирование долга и ответственности (убеждение в том, что успех урока-путешествия зависит от четкой работы каждого)

Методы контроля и самоконтроля:

— устный контроль и самоконтроль (индивидуальный и фронтальный опрос, в проверке усвоения правил, рефлексия);

— письменный контроль и самоконтроль (балльное оценивание самостоятельных и групповых работ)

— Сегодня мы продолжаем наше путешествие по стране Геометрии. А какими качествами должны обладать путешественники?

( Быть осмотрительными, внимательными, выносливыми, наблюдательными, дружными)

— Благодаря этим качествам путешественники открывают для себя что-то новое. Я надеюсь, что вы все обладаете данным набором качеств и сегодня, как настоящие путешественники, откроете для себя новые знания.

Актуализация опорных знаний

1 .Запись даты: 20 декабря.

2.Построение геометрических фигур

-Каких жителей страны Геометрии вы знаете? (круг, квадрат, прямоугольник, треугольник, прямая, угол, луч и т.д.)

— Какие операции мы научились выполнять с геометрическими фигурами? (чертить, измерять, сравнивать, находить периметр)

— Что такое периметр? (Сумма длин всех сторон)

Задание: Надо построить прямоугольник, периметр которого равен 12см . (вывесить табличку: Р=12см)

— Определим программу действий.

— С чего начнем? (Дети вспоминают алгоритм выполнения данного задания. Затем он вывешивается на доске)

2.Найти 2 таких числа, при сложении которых получится значение полуР. Эти числа и будут сторонами прямоугольника.

3.Начертить прямоугольник с полученными сторонами.

— Находим полуР: 12=6+6 (вывесить табличку) полуР = 6см

-Вспоминаем состав числа 6: 5 и 1, 4 и 2, 3 и 3. (вывесить таблички)

1-ый ряд чертит прямоугольник со сторонами 5см и 1см,

2-ой ряд – со сторонами 4см и 2см,

3-ий ряд со сторонами 3см и 3см

— Сравните свой прямоугольник с прямоугольником соседа. (В это время прикрепить к доске шаблоны прямоугольников)

2.Что такое периметр.

3.Знание алгоритма построения прямоугольника по известному периметру.

4.Знание состава чисел 12 и 6.

Если у вас возникли большие сложности при выполнении этого задания, то поставьте себе пока «-»

— У кого «5»? У кого «4»? У кого «-»?

— Молодцы, путешествуем дальше.

-В группе слов найдите лишнее слово. Почему оно лишнее? Обсудите в паре.

Килограмм слова? ( можно посоветоваться в паре )

Сантиметр Лишнее слово – килограмм, т.к. все остальные – меры

— Какие еще величины вы знаете?

Длина Объем Масса Угол Площадь

— Если вы определили лишнюю величину и вспомнили меры с помощью соседа, то поставьте «4».

— А если забыли многие величины и их меры, поставьте на полях «-».

— У кого «5»? У кого «4»? У кого «-»?

1. Определение темы урока. Постановка учебных задач.

— Посмотрите внимательно на полученную схему и попытайтесь определить тему урока-путешествия.

(На дерево понятий вывешиваются таблички со словами «Площадь» и «Единицы (меры) площади»)

— Поставьте учебные задачи (цели).

(Узнать новое о площади, познакомиться с мерами площади, научиться измерять площадь)

Работа в паре. Взаимооценка.

-Что такое площадь? ( Величина, которая указывает, сколько места занимает фигура на плоскости, называется площадью )

— Расскажите это определение в паре и оцените друг друга.

— Кому поставили «5»? Кому «4»? Кому «3»?

— Давайте вспомним, как измеряются любые величины?

(Выбирается мерка и устанавливается, сколько раз она содержится в измеряемой величине).

— Сейчас вы будете работать в группах. Послушайте, что надо сделать:

— положить перед собой желтый прямоугольник, взять конверт с надписью «мерки». В нем вы найдете меры разных геометрических форм. Ваша задача состоит в том, чтобы исследовать, какими мерами лучше, удобнее пользоваться для измерения площади желтого прямоугольника.

Вывод: Квадрат – самая удобная единица (мера) площади.

-Квадратами очень удобно замащивать плоские участки, а скажем кругами такого не сделаешь без дыр и наложений. Часто математики вместо слов «нахождение площади» говорят «квадрирование »

(На дерево понятий вывешивается табличка «квадрирование»)

— Кто понял значение этого слова? Объясните.

— Измерьте площадь желтого прямоугольника имеющимися у вас мерами-квадратами. Сколько квадратных мер у вас получилось?

— Почему так получилось?

(Дети могут предположить, что могут быть разными измеряемые прямоугольники, или используемые меры разного размера)

— Как узнать, одинаковые ли по площади ваши прямоугольники?

(С помощью наложения). Они совпали, значит, площадь их одинакова.

— Теперь покажите свои мерки-квадраты. Что вы можете о них сказать?

(Форма одинакова, а размеры разные)

— Можем ли мы теперь ответить на вопрос, почему у вас получились разные числа при измерении площади желтого прямоугольника?

(одинаковые прямоугольники измеряли разными мерами)

— Какое правило себе напомнили?

( Вспомнили, что сравнивать, складывать и вычитать величины можно только тогда, когда они измерены одинаковыми мерками.)

— Как поступить, чтобы при решении этой задачи у всех детей могли получиться одинаковые числа?

(Нужно изготовить для всех одинаковые меры и пользоваться только ими)

— Такая одинаковая (общая) для всех мера называется стандартной.

(На дерево понятий вывешивается табличка « стандартная мера »)

— В 1870 и 1872гг. международная комиссия сначала 24-х, позднее 30 государств рекомендовала создать в Париже специальное международное бюро мер и весов, которому поручается ведать изготовлением и хранением стандартных мер. Эти меры и сейчас хранятся в подвале международного бюро мер в Париже.

— У вас на партах лежат конверты с надписью « стандарт ». В них лежат стандартные меры для измерения площади. Возьмите самые маленькие из них и измерьте еще раз площадь желтого прямоугольника.

Как измерить площадь?

Стали мерки в три ряда,

Чтобы площадь нам узнать,

Нужно их пересчитать.

— Какое число у вас получилось? (18кв.)

Вывод: При измерении фигур стандартными мерами получаются одинаковые числа.

— Начертите эту меру у себя в тетради. Сколько клеточек в квадратном сантиметре? (4клетки). Обозначается эта мера так: 1см². Запишите её рядом с начерченным квадратом.

— На стр.58 найдите задание №3.Измерьте площадь каждой фигуры в квадратных сантиметрах и запишите результат.

— У кого «5»? У кого «4»? У кого «-»?

— Почему быстро удалось измерить площадь данных фигур? (фигуры уже были поделены на квадратные сантиметры)

— Измерьте площадь прямоугольников, начерченных в ваших тетрадях, разбив их на квадраты со стороной 1см. Проверьте мою работу (перевернуть прямоугольники обратной стороной, где они разделены на кв. см).

— Запишите полученные результаты. (5см²,8см², 9см²)

— Оцените мою работу (под каждым прямоугольником прикрепить карточки с результатами площадей). У кого не так?

— Вспомните, какой Р был у этих прямоугольников?

— А что можно сказать о площади этих прямоугольников? (она разная)

— Почему получились разные площади? Посоветуйтесь в парах.

(Потому что разные стороны (измерения)

— А в каком прямоугольнике наибольшая площадь? (у квадрата)

— Давайте, исследуем, почему площадь квадрата является наибольшей. Для этого найдите разницу между длиной и шириной в каждом прямоугольнике и соотнесите ее с площадью. Сделайте вывод.

Вывод: Чем меньше разница между длиной и шириной, тем больше площадь. Если разница между длиной и шириной равна 0, то это квадрат. Значит, у квадрата самая большая площадь.

— Именно по этой причине квадрат и выбран в качестве стандартной меры площади.

6.Индивидуальная работа по разноуровневым карточкам

— Кто выбрал задания 1-ого уровня? Почему? Кто 2-ого? Почему? Кто 3-его?

— У кого возникли проблемы? Какие?

Коллективная проверка и самооценка

7. Знакомство с другими мерами площади.

— В конвертах с надписью «стандарт» у вас осталась еще одна мера. Посмотрите на нее. Кто догадался, как она называется? (1дм²). Посмотрите как обозначается эта мера (показать табличку-образец). Из каких мерочек она состоит? (кв. см). Сколько их? (100)

— Как вы думаете, для чего понадобилась ещё одна мера площади? Посоветуйтесь в паре (для измерения разных по размеру площадей)

— Есть ещё одна более крупная мера, она называется кв. метр. Кто знает, как её построить? (начертить квадрат со стороной 1м)

8.«Мостик» к следующему уроку

— Кто захотел познакомиться поближе с мерами площади?

— Этим мы займёмся в наших следующих путешествиях по удивительной стране Геометрии.

— Удалось ли нам стать настоящими путешественниками и сделать новые открытия?

— Расскажите о своих открытиях в парах. А поможет вам в этом «Дерево понятий».

— Поделитесь теперь своими открытиями со мной.

— У кого «5»? У кого «4»? У кого «3»?

— Какая геометрическая фигура была главной в нашем путешествии? (квадрат)

— Возьмите свои сигнальные квадраты. Если вам понравилось сегодня путешествовать по стране Геометрии и открывать новые знания, покажите мне красные квадраты. А если у вас такого желания не возникло, покажите синий квадрат.

— Я с удовольствием сегодня путешествовала вместе с вами, спасибо!

Источник

Площадь фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см 2

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

Площадь прямоугольника

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см 2

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м 2
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см 2

S _ABC = S_ABCD : 2

S _ABC = 20 : 2 = 10 см 2

S _ABC = S _ACD = 10 см 2

Источник