поясните суть понятий кодирование код кодовая таблица

ГДЗ по информатике 10 класс учебник Босова параграф 4

1. Приведите примеры процессов обработки информации, которые чаще всего вам приходится выполнять в жизни. Для каждого примера определите исходные данные, алгоритм (правила) обработки и получаемые результаты. К каким типам обработки информации относятся эти процессы?

2. Поясните суть понятий «кодирование», «код», «кодовая таблица».

Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем.

Код — это система (список) условных обозначений (кодовых слов), используемых для представления информации.

3. Светодиодная панель содержит шесть излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?

Итак, у нас получилось 6-значное число в 4-ричной системе счисления.

Таких чисел (различных сигналов, то есть комбинаций) может быть (это ответ):

4. Автомобильный номер состоит из нескольких букв (количество букв одинаковое во всех номерах), за которыми следуют три цифры. При этом используются 10 цифр и только 5 букв: А, В, С, D и F. Требуется не менее 100 тысяч различных номеров. Какое наименьшее количество букв должно быть в автомобильном номере?

5. Сколько существует различных последовательностей из 6 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат не менее двух букв А (т. е. две и более буквы А)?

Предлагаю найти количество всех последовательностей и вычесть из них те, в которых содержится менее двух букв А.

Всего последовательностей: 4^6 = 4096

Последовательностей без буквы А: 3^6 = 729

С одной буквой А: 6 * 3^5 = 1458

6. Сравните равномерные и неравномерные коды. Каковы их основные достоинства и недостатки?

Равномерные коды легче декодировать, но закодированные сообщения будут содержать больше символов. Сообщения, закодированные неравномерными кодами, будут короче, чем на равномерных кодах, но необходимо будет для кодирования сообщения проверять код на условие Фано, и закодированное сообщение сложнее раскодировать. Так же невозможно сразу посчитав количество символов, по сравнению с равномерными кодами.

7. Какие коды называют префиксными? Почему они так важны? В чём суть прямого и обратного условий Фано?

Код называется префиксным, если ни одна из его комбинаций не является префиксом другой комбинации того же кода. Часть кодовой комбинации, которая дополняет префикс до самой комбинации, называется суффиксом. Префиксные коды наглядно могут быть представлены с помощью кодовых деревьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода.

8. Двоичные коды для 5 букв латинского алфавита представлены в таблице:

Из четырёх сообщений, закодированных этими кодами, только одно пришло без ошибки. Найдите его:

1) 110100000100110011;
2) 111010000010010011;
3) 110100001001100111;
4) 110110000100110010.

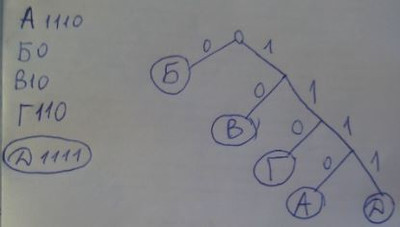
9. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. При этом используются следующие коды: А — 1110, Б — 0, В — 10, Г — 110. Каким кодовым словом может быть закодирована буква Д? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

10. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный троичный код, позволяющий однозначно декодировать полученную троичную последовательность. Вот этот код: А — 0, Б — 11, В — 20, Г — 21, Д — 22. Можно ли сократить для одной из букв длину кодового слова так, чтобы закодированную последовательность по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны.

11. Для передачи закодированных сообщений используется таблица кодовых слов из четырёх букв. Причем используются только буквы А, Р и У. Сколько различных кодовых слов может быть в такой таблице, если ни в одном слове нет трёх одинаковых букв, идущих подряд?

Различных слов длины 4, состоящих из букв А, Р и У, ровно 3 4 =81.

Выпишем все запрещённые слова. Сначала выпишем все те слова, в которых три одинаковых буквы подряд идут с позиции 1 по позицию 3:

АААА, АААР, АААУ
РРРА, РРРР, РРРУ
УУУА, УУУР, УУУУ

Теперь выпишем те, в которых одинаковые буквы стоят на позиции 2-4 (без учёта тех слов, в которых все буквы одинаковые, т.к. они были выписаны ранее)
РААА, УААА

Всего получилось 15 запрещённых слов, значит, разрешённых слов 81-15=66.

12. Методом половинного деления в последовательности чисел 061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612 требуется найти число 590. Опишите процесс поиска.

Просмотр 1. Работаем со всей последовательностью. Определяем центральный элемент (он подчёркнут):

061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем левую часть последовательности.

Просмотр 2. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):

367 389 456 478 523 567 590 612

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем левую часть последовательности.

Просмотр 3. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):

Сравниваем искомый элемент с центральным.

Центральный элемент совпадает с искомым. Поиск завершён.

13. В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии. Вот её условие.

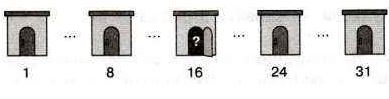
Плотник в Бобровой Деревне использует 31 склад, пронумерованный от 1 до 31. Однажды он забыл, сколько складов уже заполнил, но помнит, что заполнял их в порядке возрастания номеров.

Чтобы уменьшить количество открывания дверей, он действует следующим образом:

Сначала открывает склад со средним номером — склад № 16. Затем:

• если склад № 16 пуст, он решает искать первый незаполненный склад в промежутке от № 1 до № 15, открывает опять средний склад — склад № 8 — и повторяет процедуру;
• если склад № 16 заполнен, то нужный склад он ищет между № 17 и № 31, открывает средний склад — склад № 24 — и повторяет процедуру.

После всех действий плотник обнаружил, что заполнены были склады от № 1 до № 15 включительно. Сколько дверей ему пришлось открыть?

Решите эту задачу. Какой из рассмотренных нами методов поиска был использован героем этой задачи?

Двоичный поиск эффективно определяет положение искомого элемента (или его отсутствие) в упорядоченном наборе.

Это один из базовых и важных алгоритмов.

Если склады от №1 до №15 заполнены, то:

— когда плотник открывает склад №16, он оказывается пуст (1-ая открытая дверь);

— тогда плотник решает искать между №1 и №15, открывает склад №8, он оказывается заполнен (2-ая открытая дверь);

— теперь он ищет между №9 и №15, открывает склад №12 — он заполнен (3-ья открытая дверь);

— наконец он открывает последний склад № 15 (5-ая дверь).

Источник

ГДЗ по информатике 10 класс учебник Босова параграф 4

1. Приведите примеры процессов обработки информации, которые чаще всего вам приходится выполнять в жизни. Для каждого примера определите исходные данные, алгоритм (правила) обработки и получаемые результаты. К каким типам обработки информации относятся эти процессы?

2. Поясните суть понятий «кодирование», «код», «кодовая таблица».

Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем.

Код — это система (список) условных обозначений (кодовых слов), используемых для представления информации.

3. Светодиодная панель содержит шесть излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?

Итак, у нас получилось 6-значное число в 4-ричной системе счисления.

Таких чисел (различных сигналов, то есть комбинаций) может быть (это ответ):

4. Автомобильный номер состоит из нескольких букв (количество букв одинаковое во всех номерах), за которыми следуют три цифры. При этом используются 10 цифр и только 5 букв: А, В, С, D и F. Требуется не менее 100 тысяч различных номеров. Какое наименьшее количество букв должно быть в автомобильном номере?

5. Сколько существует различных последовательностей из 6 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат не менее двух букв А (т. е. две и более буквы А)?

Предлагаю найти количество всех последовательностей и вычесть из них те, в которых содержится менее двух букв А.

Всего последовательностей: 4^6 = 4096

Последовательностей без буквы А: 3^6 = 729

С одной буквой А: 6 * 3^5 = 1458

6. Сравните равномерные и неравномерные коды. Каковы их основные достоинства и недостатки?

Равномерные коды легче декодировать, но закодированные сообщения будут содержать больше символов. Сообщения, закодированные неравномерными кодами, будут короче, чем на равномерных кодах, но необходимо будет для кодирования сообщения проверять код на условие Фано, и закодированное сообщение сложнее раскодировать. Так же невозможно сразу посчитав количество символов, по сравнению с равномерными кодами.

7. Какие коды называют префиксными? Почему они так важны? В чём суть прямого и обратного условий Фано?

Код называется префиксным, если ни одна из его комбинаций не является префиксом другой комбинации того же кода. Часть кодовой комбинации, которая дополняет префикс до самой комбинации, называется суффиксом. Префиксные коды наглядно могут быть представлены с помощью кодовых деревьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода.

8. Двоичные коды для 5 букв латинского алфавита представлены в таблице:

Из четырёх сообщений, закодированных этими кодами, только одно пришло без ошибки. Найдите его:

1) 110100000100110011;
2) 111010000010010011;
3) 110100001001100111;
4) 110110000100110010.

9. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. При этом используются следующие коды: А — 1110, Б — 0, В — 10, Г — 110. Каким кодовым словом может быть закодирована буква Д? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

10. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный троичный код, позволяющий однозначно декодировать полученную троичную последовательность. Вот этот код: А — 0, Б — 11, В — 20, Г — 21, Д — 22. Можно ли сократить для одной из букв длину кодового слова так, чтобы закодированную последовательность по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны.

11. Для передачи закодированных сообщений используется таблица кодовых слов из четырёх букв. Причем используются только буквы А, Р и У. Сколько различных кодовых слов может быть в такой таблице, если ни в одном слове нет трёх одинаковых букв, идущих подряд?

Различных слов длины 4, состоящих из букв А, Р и У, ровно 3 4 =81.

Выпишем все запрещённые слова. Сначала выпишем все те слова, в которых три одинаковых буквы подряд идут с позиции 1 по позицию 3:

АААА, АААР, АААУ
РРРА, РРРР, РРРУ
УУУА, УУУР, УУУУ

Теперь выпишем те, в которых одинаковые буквы стоят на позиции 2-4 (без учёта тех слов, в которых все буквы одинаковые, т.к. они были выписаны ранее)
РААА, УААА

Всего получилось 15 запрещённых слов, значит, разрешённых слов 81-15=66.

12. Методом половинного деления в последовательности чисел 061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612 требуется найти число 590. Опишите процесс поиска.

Просмотр 1. Работаем со всей последовательностью. Определяем центральный элемент (он подчёркнут):

061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем левую часть последовательности.

Просмотр 2. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):

367 389 456 478 523 567 590 612

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем левую часть последовательности.

Просмотр 3. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):

Сравниваем искомый элемент с центральным.

Центральный элемент совпадает с искомым. Поиск завершён.

13. В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии. Вот её условие.

Плотник в Бобровой Деревне использует 31 склад, пронумерованный от 1 до 31. Однажды он забыл, сколько складов уже заполнил, но помнит, что заполнял их в порядке возрастания номеров.

Чтобы уменьшить количество открывания дверей, он действует следующим образом:

Сначала открывает склад со средним номером — склад № 16. Затем:

• если склад № 16 пуст, он решает искать первый незаполненный склад в промежутке от № 1 до № 15, открывает опять средний склад — склад № 8 — и повторяет процедуру;
• если склад № 16 заполнен, то нужный склад он ищет между № 17 и № 31, открывает средний склад — склад № 24 — и повторяет процедуру.

После всех действий плотник обнаружил, что заполнены были склады от № 1 до № 15 включительно. Сколько дверей ему пришлось открыть?

Решите эту задачу. Какой из рассмотренных нами методов поиска был использован героем этой задачи?

Двоичный поиск эффективно определяет положение искомого элемента (или его отсутствие) в упорядоченном наборе.

Это один из базовых и важных алгоритмов.

Если склады от №1 до №15 заполнены, то:

— когда плотник открывает склад №16, он оказывается пуст (1-ая открытая дверь);

— тогда плотник решает искать между №1 и №15, открывает склад №8, он оказывается заполнен (2-ая открытая дверь);

— теперь он ищет между №9 и №15, открывает склад №12 — он заполнен (3-ья открытая дверь);

— наконец он открывает последний склад № 15 (5-ая дверь).

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Обработка информации

§ 4. Обработка информации

Информатика. 10 класса. Босова Л.Л. Оглавление

Информационный процесс — совокупность последовательных действий (операций), производимых над информацией (в виде данных, фактов, идей, гипотез, теорий и пр.) для получения какого-либо результата (достижения цели).

Можно выделить три основных типа информационных процессов: обработка, хранение и передача информации. Рассмотрим их подробнее.

Обработка информации — это целенаправленный процесс изменения содержания или формы представления информации.

Хранение информации – это один из главных информационных процессов, с которым неразрывно связано понятие устройства хранения информации, или запоминающего устройства. Разные устройства могут использовать различные способы хранения информации.

Передача информации — физический процесс, посредством которого осуществляется перемещение информации в пространстве. Записали информацию на диск и перенесли в другую комнату.

Данный процесс характеризуется наличием следующих компонентов:

Источник информации.
Приёмник информации.
Носитель информации.
Среда передачи.

4.1. Задачи обработки информации

Из курса информатики основной школы вам известно, что существует два различных типа обработки информации: 1) обработка, связанная с получением нового содержания, новой информации; 2) обработка, связанная с изменением формы представления информации, не изменяющая её содержания.

К первому типу обработки информации относятся: преобразование по правилам (в том числе вычисления по формулам), исследование объектов познания по их моделям, логические рассуждения, обобщение и др.

Ко второму типу обработки информации можно отнести: • кодирование — переход от одной формы представления информации к другой, более удобной для восприятия, хранения, передачи или последующей обработки; • структурирование — организацию информации по некоторому правилу, связывающему её в единое целое; • поиск и отбор информации, требуемой для решения некоторой задачи, из информационного массива и др.

При всём многообразии решаемых задач в процессе обработки информации всегда решается некоторая информационная задача, а именно: дан некоторый набор исходных данных — исходной информации, требуется получить некоторые результаты — итоговую информацию. Сам процесс перехода от исходных данных к результату и есть процесс обработки. Тот объект, который осуществляет обработку, может быть назван исполнителем обработки. Для успешного выполнения обработки информации исполнителю должен быть известен способ обработки, т. е. последовательность действий, которую нужно выполнить, чтобы достичь нужного результата. Описание такой последовательности принято называть алгоритмом обработки.

Общая схема процесса обработки информации представлена на рисунке 1.11.

Рис. 1.11. Общая схема процесса обработки информации

Исполнителем обработки информации может быть человек или компьютер. При этом человек, как правило, является неформальным, творчески действующим исполнителем. Даже для решения самой простой математической задачи разные люди могут использовать разные способы!

Что касается компьютера, то он является формальным исполнителем, действия которого осуществляются автоматически, строго в соответствии с имеющимся алгоритмом обработки информации.

Рассмотрим отдельные процессы обработки информации более подробно.

4.2. Кодирование информации

Кодирование информации широко используется в технических средствах работы с информацией (телеграф, радио, компьютеры).

Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем.

Кодовая таблица — это совокупность используемых кодовых слов и их значений.

1) Также кодом зачастую называют результат кодирования информации.

Ранее мы уже рассмотрели примеры равномерных двоичных кодов — пятиразрядный код Бодо и восьмиразрядный код ASCII.

Самый известный пример неравномерного кода — код (азбука) Морзе, в которой цифры и буквы алфавита представляются последовательностями длинных («тире») и коротких («точек») сигналов, названный в честь американского изобретателя и художника Сэмюэля Морзе (1791-1872). Буквы, встречающиеся в сообщениях чаще, имеют в этом коде более короткий код, чем «редкие» буквы (рис. 1.12).

Рис. 1.12. Кодовая таблица азбуки Морзе

В азбуке Морзе сигналы отделяются друг от друга паузами — отсутствием сигналов. За единицу «измерения» длительности сигналов принимается длительность сигнала «точка». Длительность тире (длинного сигнала) равна длительности трёх точек (коротких сигналов). Пауза между сигналами одного знака равна одной точке; пауза между знаками в слове — трём точкам; пауза между словами — семи точкам. Фактически пауза является третьим знаком в азбуке Морзе, а сам код — троичным.

Слово WORD, закодированное с помощью азбуки Морзе, на «временной» шкале можно представить так:

Самым знаменитым сообщением, закодированным азбукой Морзе, является сигнал бедствия «SOS». Его запрещено использовать без острой на то необходимости. Передаётся сигнал без межбуквенных пауз:

При использовании неравномерных кодов важно понимать, сколько различных кодовых слов они позволяют построить.

Пример 1. Светодиодная панель содержит восемь излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или синим, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?

На уроках математики и информатики в основной школе вы изучали элементы комбинаторики, в том числе правило умножения. Согласно ему, если элемент А можно выбрать n способами и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами. Это правило справедливо и для произвольного количества независимо выбираемых элементов.

Применим его к решению нашей задачи.

Существует 4 варианта выбора цвета первого элемента, 4 варианта выбора цвета второго элемента; цвета для пары элементов (1, 2) можно выбрать 4 • 4 = 4 2 = 16 способами; цвета для тройки элементов (1, 2, 3) можно выбрать 16 • 4 = 4 3 = 64 способами и т. д. Цвета для восьми элементов (1, 2, 3, 4, 5, 6, 7, 8) можно выбрать 4 8 = 65 536 способами.

Можно ли отнести эту задачу к классу задач на определение максимально возможного количества комбинаций (слов) фиксированной длины определённого алфавита? Обоснуйте свой ответ.

Пример 2. Выясним, сколько всего различных символов можно закодировать, используя последовательности точек и тире, содержащие не более шести знаков.

Для кодирования различных символов можно использовать последовательности точек и тире, содержащие не более шести знаков, т. е. 1, 2, 3, 4, 5 или 6 знаков.

Последовательностями, содержащими один из двух возможных знаков, можно закодировать два символа: один будет закодирован точкой, второй — тире.

Рассмотрим последовательности, содержащие два знака из двухсимвольного алфавита. Их может быть 2 • 2 = 2 2 = 4.

Последовательностей из трёх знаков, принадлежащих двухсимвольному алфавиту, может быть 4 • 2 = 2 3 = 8.

Рассуждая аналогичным образом, подсчитаем число последовательностей, содержащих 4, 5 и 6 знаков — 16, 32 и 64 соответственно.

Число различных последовательностей, содержащих не более шести знаков двухсимвольного алфавита, будет равно 126 = 2 + 4 + 8 + 16 + 32 + 64.

Пример 3. Имеющаяся информация должна быть закодирована в четырёхбуквенном алфавите <А, В, С, D>. Выясним, сколько существует различных последовательностей из 7 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат ровно пять букв А.

Нас интересуют семисимвольные последовательности, любые пять мест в которых будут заняты буквой А, а на двух оставшихся местах могут находиться любые из букв В, С, D.

Так как на 6-м и 7-м местах могут стоять любые из трёх оставшихся букв В, С, D, то всего существует 9 (3 • 3 = 9) разных семибуквенных последовательностей, в которых первые пять позиций заняты буквой А.

Но ведь буквы А могут находиться на любых пяти из имеющихся семи позиций. Например:

А сколько таких вариантов всего? Сколько всего существует способов, которыми мы можем выбрать пять мест из семи для размещения там буквы А?

Для ответа на этот вопрос нужно вспомнить некоторые сведения из изученного в основной школе раздела математики, называемого комбинаторикой.

В комбинаторике набор k элементов, выбранных из данного множества, содержащего n различных элементов, называется сочетанием из n по k.

Для вычисления значения этой величины применяется формула:

Здесь n! = 1 • 2 • … • n.

Действительно, множество, с которым мы имеем дело, состоит из мест для записи символов в последовательности. Его элементы можно обозначить 1, 2, 3, 4, 5, 6 и 7. Требуётся выбрать из этого множества пять мест для размещения буквы А. Число возможных вариантов можно вычислить как число сочетаний из 7 по 5:

Итак, существует 21 вариант выбора в семибуквенной последовательности ровно пяти мест для размещения там буквы А. Для каждого из этих 21 вариантов имеется 9 разных вариантов заполнения двух оставшихся мест.

Всего существует 189 (21 • 9 = 189) различных последовательностей из 7 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат ровно пять букв А.

Главное условие использования неравномерных кодов — возможность однозначного декодирования записанного с их помощью сообщения. Именно поэтому в технических системах широкое распространение получили префиксные коды: они состоят из слов разной длины, записываемых без разделительного символа. При этом сообщение, закодированное с их помощью, может быть однозначно декодировано.

Прёфиксный код — код со словом переменной длины, обладающий тем свойством, что никакое его кодовое слово не может быть началом другого (более длинного) кодового слова.

1) код, состоящий из слов 0, 10 и 11, является префиксным;
2) код, состоящий из слов 0, 10, 11 и 100, не является префиксным.

Для того чтобы сообщение, записанное с помощью неравномерного кода, однозначно декодировалось, достаточно, чтобы никакое кодовое слово не было началом другого (более длинного) кодового слова. Это условие ещё называют условием Фано (в честь Роберта Марио Фано, американского учёного, известного по работам в области теории информации).

Обратное условие Фано также является достаточным условием однозначного декодирования неравномерного кода. В нём требуется, чтобы никакой код не был окончанием другого (более длинного) кода.

Для возможности однозначного декодирования достаточно выполнения одного из условий Фано — или прямого, или обратного.

Как вы понимаете смысл этого утверждения? Можно ли на его основе заявлять, что если для некоторого кода условие Фано не выполняется, то однозначное декодирование записанного с его помощью сообщения невозможно?

Пример 4. Двоичные коды для 5 букв латинского алфавита представлены в таблице:

Выясним, какое сообщение (какой набор букв) закодировано с помощью этих кодов двоичной строкой: 0110100011000.

Проанализируем имеющиеся коды: код буквы В (01) является началом кода буквы Е (011); код буквы D (10) является началом кода буквы С (100).

Таким образом, прямое условие Фано для заданных кодов не выполняется. Следовательно, имеющуюся двоичную строку нельзя декодировать однозначно, если начать её декодирование с начала (слева направо).

Начните проводить декодирование двоичной строки 0110100011000 слева направо и убедитесь в справедливости условия Фано.

Для имеющихся кодов выполняется обратное условие Фано: никакой код не является окончанием другого кода. Следовательно, имеющуюся двоичную строку можно декодировать однозначно, если начать её декодирование с конца (справа налево).

Итак, направление однозначного декодирования установлено. Процесс декодирования может быть представлен так:

Если для некоторой последовательности кодов выполняется прямое условие Фано, то её декодирование следует вести слева направо. Если для некоторой последовательности кодов выполняется обратное условие Фано, то её декодирование следует вести справа налево.

Из курса информатики основной школы вам знакомо понятие дерева — иерархической структуры, состоящей из набора вершин и рёбер. Вершина, в которую не входит ни одного ребра, называется корнем; вершины, из которых не выходит ни одного ребра, называются листьями.

Дерево, из вершин которого выходит только два ребра, называется двоичным (бинарным) деревом.

Комбинации, соответствующие листьям бинарного дерева, являются кодовыми комбинациями префиксного кода.

Префиксные коды можно наглядно представить с помощью кодовых деревьев.

Пример 5. Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Для букв А, Б и В использовали такие кодовые слова: А — О, Б — 10, В — 110.

Каким кодовым словом может быть закодирована буква Г? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

Для решения задачи воспользуемся бинарным деревом.

Отметим вершины, соответствующие используемым кодовым словам: А — 0, Б — 10, В — 110:

Так как комбинациям префиксного кода должны соответствовать листья бинарного дерева, наше кодовое дерево должно выглядеть так:

Итак, для кодирования буквы Г можно использовать код 111.

Усложним условие задачи. Теперь кодируемая последовательность состоит из букв А, Б, В, Г и Д. Кодовые слова для букв А, Б и В определены: А — О, Б — 10, В — 110.

Какими кодовыми словами могут быть закодированы буквы Г и Д? Код должен удовлетворять свойству однозначного декодирования. Общая длина кодовых слов для всех пяти букв должна быть минимальной.

4.3. Поиск информации

Неоценима роль компьютера в организации важнейшей задачи обработки информации — поиска информации, необходимой человеку для решения стоящей перед ним задачи.

Вспомните, как часто и какую информацию приходится искать вам, членам вашей семьи, вашим друзьям и знакомым. Приведите примеры.

Задача поиска обычно формулируется следующим образом. Имеется некоторое хранилище информации — информационный массив (телефонный справочник, словарь, расписание поездов, диск с файлами и др.). Требуется найти в нём нужную информацию, удовлетворяющую определённым условиям поиска (телефон данной организации, перевод данного слова на английский язык, время отправления данного поезда, файл с рефератом). При этом, как правило, необходимо сократить время поиска, которое зависит от способа организации набора данных и используемого алгоритма поиска.

Алгоритм поиска, в свою очередь, зависит от способа организации информации.

Если данные никак не организованы, то мы имеем дело с неструктурированным набором данных. Для осуществления поиска в таком наборе данных применяется метод последовательного перебора: все элементы, начиная с первого, просматриваются подряд. Поиск завершается в двух случаях:

1) искомый элемент найден, при этом может быть просмотрена как часть имеющегося набора данных, так и весь набор, если искомый элемент оказался последним в наборе;
2) просмотрены все элементы имеющегося набора данных, но искомого элемента среди них не оказалось.

Длительность поиска методом последовательного перебора определяется как N/2, где N — размер набора данных. Действительно, искомый элемент может оказаться первым среди просматриваемых, и в этом случае длительность поиска равна 1. Если искомый элемент окажется последним или его не окажется вообще, то длительность поиска будет равна N. Если провести поиск последовательным перебором достаточно много раз, то окажется, что в среднем на поиск требуемого элемента уходит N/2 просмотров.

Гораздо проще осуществлять поиск в структурированном наборе данных. Структурирование связано с внесением определённого порядка, определённой организации: расположения данных в алфавитном порядке, группировки по некоторым признакам и т. д. Если информация структурирована, то поиск осуществляется быстрее, можно построить оптимальный алгоритм.

Ранее мы уже рассматривали метод половинного деления. Он применяется к наборам данных, элементы которых упорядочены по неубыванию, т. е. каждый последующий элемент не меньше (больше или равен) предыдущего:

Искомый элемент сравнивается с центральным элементом последовательности, номер которого находится как [N/2] + 1. Квадратные скобки здесь обозначают, что от результата деления берётся только целая часть, а дробная часть отбрасывается.

Если искомый элемент больше центрального, то поиск продолжается в правой части последовательности. Если искомый элемент меньше центрального, то — в левой. Если значения искомого элемента и центрального совпадают, то поиск завершается.

Рассмотрим работу этого алгоритма поиска информации на примере.

Пример 6. В последовательности чисел

061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612

требуется найти число 180.

Просмотр 1. Работаем со всей последовательностью. Определяем центральный элемент (он подчёркнут):

061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем правую часть последовательности.

Просмотр 2. Работаем с левой частью последовательности. Определяем центральный элемент (он подчёркнут):

061 087 154 180 208 230 290 345

Сравниваем искомый элемент с центральным.

Просмотр 3. Работаем с левой частью последовательности. Определяем центральный элемент (он подчёркнут):

061 087 154 180

Сравниваем искомый элемент с центральным.

По результатам сравнения отбрасываем левую часть последовательности.

Просмотр 4. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):

Центральный элемент совпадает с искомым. Поиск завершён.

Как связаны длительность поиска методом половинного деления и длина исходной последовательности данных?

САМОЕ ГЛАВНОЕ

Обработка информации — это целенаправленный процесс изменения содержания или формы представления информации. Существует два различных типа обработки информации:

1) обработка, связанная с получением нового содержания, новой информации;
2) обработка, связанная с изменением формы представления информации, не изменяющая её содержания.

Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем.

Код — это система (список) условных обозначений (кодовых слов), используемых для представления информации.

Префиксный код — код со словом переменной длины, обладающий тем свойством, что никакое его кодовое слово не может быть началом другого (более длинного) кодового слова. Сообщение, закодированное с помощью префиксного кода, может быть однозначно декодировано.

Задача поиска информации состоит в том, чтобы в некотором хранилище информации (информационном массиве) найти информацию, удовлетворяющую определённым условиям поиска.

Время поиска зависит от способа организации набора данных и используемого алгоритма поиска.

Для осуществления поиска в неструктурированном наборе данных применяется метод последовательного перебора.

Поиск информации в упорядоченном по неубыванию наборе данных может быть осуществлён методом половинного деления.

Вопросы и задания

1. Приведите примеры процессов обработки информации, которые чаще всего вам приходится выполнять в жизни. Для каждого примера определите исходные данные, алгоритм (правила) обработки и получаемые результаты. К каким типам обработки информации относятся эти процессы?

2. Поясните суть понятий «кодирование», «код», «кодовая таблица».

3. Светодиодная панель содержит шесть излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?

4. Автомобильный номер состоит из нескольких букв (количество букв одинаковое во всех номерах), за которыми следуют три цифры. При этом используются 10 цифр и только 5 букв: А, В, С, D и F. Требуется не менее 100 тысяч различных номеров. Какое наименьшее количество букв должно быть в автомобильном номере?

5. Сколько существует различных последовательностей из 6 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат не менее двух букв А (т. е. две и более буквы А)?

6. Сравните равномерные и неравномерные коды. Каковы их основные достоинства и недостатки?

7. Какие коды называют префиксными? Почему они так важны? В чём суть прямого и обратного условий Фано?

8. Двоичные коды для 5 букв латинского алфавита представлены в таблице:

Из четырёх сообщений, закодированных этими кодами, только одно пришло без ошибки. Найдите его:

1) 110100000100110011;
2) 111010000010010011;
3) 110100001001100111;
4) 110110000100110010.

9. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. При этом используются следующие коды: А — 1110, Б — 0, В — 10, Г — 110. Каким кодовым словом может быть закодирована буква Д? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

10. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный троичный код, позволяющий однозначно декодировать полученную троичную последовательность. Вот этот код: А — 0, Б — 11, В — 20, Г — 21, Д — 22. Можно ли сократить для одной из букв длину кодового слова так, чтобы закодированную последовательность по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны.

11. Для передачи закодированных сообщений используется таблица кодовых слов из четырёх букв. Причем используются только буквы А, Р и У. Сколько различных кодовых слов может быть в такой таблице, если ни в одном слове нет трёх одинаковых букв, идущих подряд?

12. Методом половинного деления в последовательности чисел

061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612

требуется найти число 590. Опишите процесс поиска.

13. В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии. Вот её условие.

Плотник в Бобровой Деревне использует 31 склад, пронумерованный от 1 до 31. Однажды он забыл, сколько складов уже заполнил, но помнит, что заполнял их в порядке возрастания номеров.

Чтобы уменьшить количество открывания дверей, он действует следующим образом:

Сначала открывает склад со средним номером — склад № 16. Затем:

• если склад № 16 пуст, он решает искать первый незаполненный склад в промежутке от № 1 до № 15, открывает опять средний склад — склад № 8 — и повторяет процедуру;
• если склад № 16 заполнен, то нужный склад он ищет между № 17 и № 31, открывает средний склад — склад № 24 — и повторяет процедуру.

После всех действий плотник обнаружил, что заполнены были склады от № 1 до № 15 включительно. Сколько дверей ему пришлось открыть?

Решите эту задачу. Какой из рассмотренных нами методов поиска был использован героем этой задачи?

Источник