Постулат в геометрии что это
а к с и о м а
постулат в геометрии
• бесспорная, не требующая доказательств истина
• доказательство без доказательства
• исходная бездоказательность, истина, не требующая доказательств
• не требующее доказательства утверждение
• полная недоказуемость, равная полной неопровержимости. Александр Круглов
• положение, принимаемое без логического доказательства
• утверждение, которое неопровержимо, пока в нем хватает соединительной силы
• у древних греков, таких как Пифагор и Евклид, это слово означало «то, что достойно почести»
• полная недоказуемость, равная полной неопровержимости
• истина, на которую не хватило доказательств
• само собой разумеющееся
• положение, не требующее доказательств
• принятая в науке истина
• постулат в математике
• догма в математике
• положение, принимаемое без доказательств
• не требует доказательств
• положение, принимаемое без доказ.
• истиное исходное положение теории
• истинное исходное положение теории
• Истина, не требующая доказательства
• Исходное положение какой-либо теории или науки, принимаемое без доказательств
• Положение, принимаемое без доказательств
• ж. греч. очевидность, ясная по себе и бесспорная истина, не требующая доказательств, напр. целое всегда, больше части своей; основная истина, самоистина, ясноистина
• положение не требующее доказательств
• положение, принимаемое без доказ
• у древних греков, таких как Пифагор и Евклид, это слово означало «то, что достойно почести»
Евклидова (элементарная) геометрия
Евклидова геометрия — это геометрическая теория, основанная на системе аксиом, которая была впервые изложена в третьем веке до нашей эры великим древнегреческим математиком Евклидом в грандиозном научном труде «Начала».
Система аксиом Евклида базируется на основных геометрические понятиях таких, как точка, прямая, плоскость, движение, а также на следующие отношения: «точка лежит на прямой на плоскости», «точка лежит между двумя другими».
В «Началах» Евклид представил следующую аксиоматику:
Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.
В современной трактовке система аксиом Евклида может быть разделена на пять групп:
Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.
Как вы находите постулат?
Если у вас есть линейный сегмент с конечными точками A и B, а точка C находится между точками A и B, тогда AC + CB = AB. Сложение угла Постулат: Это постулаты утверждает, что если вы разделите один угол на два меньших угла, то сумма этих двух углов должна быть равна величине исходного угла.
Принимая это во внимание, как найти смежные углы?
Две углов Он Смежный когда они имеют общую сторону и общую вершину (угловую точку) и не перекрываются. Потому что: у них общая сторона (линия CB) у них есть общая вершина (точка B)
Также знайте, что такое постулат SSS? Доказательство конгруэнтных треугольников с помощью SSS. Сторона Сторона Сторона постулат утверждает, что если три стороны одного треугольника конгруэнтны трем сторонам другого треугольника, то эти два треугольника конгруэнтны.
Как разделить угол пополам?
Какие 5 постулатов в геометрии?
Как вы решаете постулаты?
Если у вас есть линейный сегмент с конечными точками A и B, а точка C находится между точками A и B, тогда AC + CB = AB. Сложение угла Постулат: Это постулаты утверждает, что если вы разделите один угол на два меньших угла, то сумма этих двух углов должна быть равна величине исходного угла.
Какова формула постулата сложения сегментов?
постулат сложения сегментов утверждает, что если нам даны две точки на линии сегмент, A и C третья точка B лежит на прямой сегмент AC тогда и только тогда, когда расстояния между точками удовлетворяют требованиям уравнения AB + BC = AC.
Каковы 11 постулатов геометрии?
| A | B |
|---|---|
| # 8. | Через любые 3 неколлинеарные точки существует ровно одна плоскость. |
| # 9. | На плоскости есть не менее трех неколлинеарных точек. |
| # 10. | Если 2 точки лежат на плоскости, то линия, содержащая их, лежит на плоскости. |
| # 11. | Если две плоскости пересекаются, то их пересечение является линией. |
Что такое перпендикулярная линия?
Какие 7 постулатов?
В чем разница между постулатом и аксиомой?
Как сложение связано с измерением угла?
Как вы определяете углы?
В плоской геометрии угол фигура, образованная двумя лучами, называемыми сторонами угол, разделяя общую конечную точку, называемую вершиной угол. Углы образованные двумя лучами, лежат в плоскости, но эта плоскость не обязательно должна быть евклидовой.
Сколько теорем в геометрии?
Каковы свойства угла?
Каждый угол противоположен другому и образуют пару так называемых противоположных углов. Углы а и с противоположны углов. Напротив углов равны. Противоположный углов иногда называют вертикальными углов или вертикально напротив углов.
Сколько существует типов постулатов?
Какие 5 постулатов в геометрии?
Что такое свойство сложения углов?
конгруэнтный. Углы конгруэнтный когда они одного размера (в градусах или радианах). Стороны конгруэнтный когда они одинаковой длины.
Что такое свойство сложения углов?
Что такое определение в геометрии?
существительное. В определение of геометрия это раздел математики, который фокусируется на измерении и соотношении линий, углов, поверхностей, тел и точек. Пример геометрия вычисление углов треугольника. YourDictionary определение и пример использования.
Конгруэнтны ли параллельные линии?
Если два параллельные линии пересекаются трансверсалью, соответствующие углы равны конгруэнтный. Если два линий пересекаются трансверсалью, а соответствующие углы равны конгруэнтный, линии параллельны. Внутренние углы на одной стороне поперечного сечения: Название представляет собой описание «местоположения» этих углов.
Какие бывают типы теорем?
Что такое постулат двух точек?
2 Точечный постулат: Через любые две точки существует ровно одна линия. Теорема о пересечении прямых: если два линии пересекаются, затем они пересекаются ровно в одном точка.
Какие углы совпадают?
Конгруэнтные углы двое или больше углов которые имеют такую же меру. Проще говоря, у них одинаковое количество степеней. Важно отметить, что длина угловкрая или направление углов не влияет на их соответствие. Пока их мера равна, углов считаются конгруэнтный.
Как разделить угол пополам?
Что такое перпендикулярная линия?
Что такое перпендикулярная линия?
сложение углов постулат гласит, что если точка находится внутри угол и вы добавляете два углов которые сделаны путем проведения линии через точку, в которой сумма будет равна большому угол, Два или более углов разделяющие одну сторону называются Соседними Углы.
Что такое постулат сложения ARC?
полукруг дуга что меры. Постулат сложения дуги Постулат сложения дуги заявляет, что мера дуга образованный двумя соседними дуги это сумма мер двух дуги.
Как читать транспортир?
Сколько постулатов в геометрии?
Есть ли постулат вычитания угла?
Там четыре вычитание теоремы, которые вы можете использовать в доказательствах геометрии: две для отрезков и две для углов. Каждому из них соответствует одна из теорем сложения. Вот вычитание теоремы для трех отрезков и трех углов (сокращенно сегмент вычитание, вычитание углаИли просто вычитание):
Какие углы совпадают?
Как читать транспортир?
Что такое постулат сложения ARC?
Конгруэнтные углы двое или больше углов которые имеют такую же меру. Проще говоря, у них одинаковое количество степеней. Важно отметить, что длина угловкрая или направление углов не влияет на их соответствие. Пока их мера равна, углов считаются конгруэнтный.
Постулаты Евклида
1.2 Постулаты Евклида
Евклид – автор первого дошедшего до нас строгого логического построения геометрии. В нем изложение настолько безупречно для своего времени, что в течение двух тысяч лет с момента появления его труда «Начал» оно было единственным руководством для изучающих геометрию.
«Начала» состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении.
Каждая книга «Начал» начинается определением понятий, которые встречаются впервые. Так, например, первой книге предпосланы 23 определения. В частности,
Определение 1. Точка есть то, что не имеет частей.
Определение 2. Линия есть длины без ширины
Определение 3. Границы линии суть точки.
Вслед за определениями Евклид приводит постулаты и аксиомы, то есть утверждения, принимаемые без доказательства.
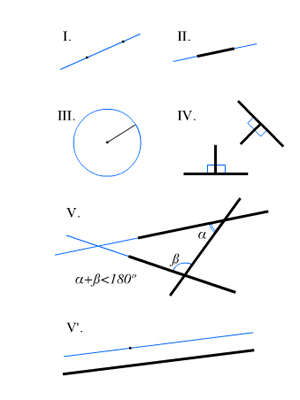
I. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.
III. И чтобы из любого центра можно было описать окружность любым радиусом.
IV. И чтобы все прямые углы были равны.
V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
I. Равные порознь третьему равны между собой.
II. И если к ним прибавим равные, то получим равные.
III. И если от равных отнимем равные, то получим равные.
IV. И если к неравным прибавим равные, то получим неравные.
V. И если удвоим равные, то получим равные.
VI. И половины равных равны между собой.
VII. И совмещающиеся равны.
VIII. И целое больше части.
IX. И две прямые не могут заключать пространства.
Иногда IV и V постулаты относят к числу аксиом. Поэтому пятый постулат иногда называют XI аксиомой. По какому принципу одни утверждения относятся к постулатам, а другие к аксиомам, неизвестно.
Никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже с древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых.
Возможно, что уже сам Евклид пытался доказать постулат о параллельных. В пользу этого говорит то обстоятельство, что первые 28 предложений «Начал» не опираются на V постулат. Евклид как бы старался отодвинуть применение этого постулата до тех пор, пока использование его не станет настоятельно необходимым.
Одни математики старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату.
Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. Так, например, в XI веке Омар Хайям ввел вместо V постулата «принцип», согласно которому две лежащие в одной плоскости сходящиеся прямые пересекаются и не могут расходиться в направлении схождения. С помощью этого принципа Хайям доказывает, что в четырехугольнике ABCD, в котором углы при основании А и В – прямые и стороны АС, ВD равны, углы С и D так же прямые, а из этого предложения о существовании прямоугольника выводится V постулат. Рассуждения Хайяма получили оригинальное развитие в XIII веке у Насирэдинна ат-Туси, работы которого в свою очередь стимулировали исследования Д. Валлиса. В 1663 году Валлис доказал постулат о параллельных, исходя из явного допущения, что для каждой фигуры существует подобная ей фигура произвольной величины. Это допущение он считал вытекающим из существа пространственных отношений.
С логической точки зрения результаты Хайяма или Валлиса лишь выявляли равносильность V постулата и некоторых других предложений геометрии. Так, Хайям, по существу, установил эквивалентность постулата и предложения о сумме углов треугольника, а Валлис показал, что не только из V постулата можно вывести учение о подобии, но и обратно – их евклидова учения о подобии следует V постулат.
Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались многие геометры XVIII и первой половины XIX веков, состоит в том, что пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию. Опираясь на измененную таким образом систему постулатов и аксиом, доказываются всевозможные предложения, логически из нее вытекающие. Если пятый постулат действительно вытекает из остальных постулатов и аксиом, то измененная указанным образом система постулатов ми аксиом противоречива. Поэтому рано или поздно мы придем у двум взаимно исключающим выводам. Этим и будет доказан пятый постулат.
Именно таким путем пытались доказать пятый постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) и А.М. Лежандр (1752-1833).
Исследования Саккери были опубликованы в 1733 году под названием «Евклид, очищенный от всяких пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии».
Саккери исходил из рассмотрения четырехугольника 
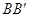
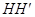
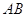
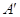
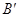
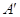
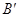
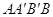
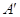
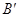
Идеи Ламберта, развитые им в сочинении «теория параллельных линий» (1766г.), близко примыкают к соображениям Саккери.
Он рассматривает четырехугольник с тремя прямыми углами. Относительно четвертого угла так же возникают три гипотезы: этот угол прямой, тупой или острый. Доказав эквивалентность пятого постулата гипотезе прямого угла и сведя к противоречию гипотезу тупого угла, Ламберт, подобно Саккери, вынужден заниматься гипотезой острого угла. Она приводит Ламберта к сложной геометрической системе, в которой ему не удалось встретить логического противоречия. Ламберт нигде в своем сочинении не утверждает, что V постулат им доказан, и приходит к твердому заключению, что и все другие попытки в этом направлении не привели к цели.
Более того, развивая систему гипотезы острого угла, Ламберт обнаруживает аналогию этой системы со сферической геометрией и в этом усматривает возможность ее существования.
«Я склонен даже думать, что третья гипотеза справедлива на какой-нибудь мнимой сфере. Должна же быть причина, вследствие которой она на плоскости далеко не поддается опровержению, как это легко может быть сделано со второй гипотезой».
Лежандр в своем доказательстве пятого постулата рассматривает три гипотезы относительно суммы углов треугольника.
1. Сумма углов треугольника равна двум прямым.
2. Сумма углов треугольника больше двух прямых.
3. Сумма углов треугольника меньше двух прямых.
Он доказал, что первая гипотеза эквивалентна пятому постулату, вторая гипотеза невозможна; и приняв третью гипотезу приходит к противоречию, неявно воспользовавшись в доказательстве пятым постулатом через один из его эквивалентов.
В результате проблема параллельных оставалась к началу XIX века неразрешенной и положение казалось безвыходным. Большой знаток вопроса венгерский математик Фаркаш Бояи в 1820 году писал своему сыну Яношу: «Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил… Этот беспросветный мрак… никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Это большая и вечная рана в моей душе…». Беспросветный мрак, о котором с горечью писал старший Бойяи, рассеял Лобачевский и, несколько позднее, Я. Бояи.
Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в России носит имя Лобачевского, который впервые опубликовал работу с ее изложением.
И одной из предпосылок геометрических открытий Н. И. Лобачевского (1792-1856) был как раз его материалистический подход к проблемам познания. Лобачевский Он был твердо уверен в объективном и не зависящем от человеческого сознания существовании материального мира и в возможности его познания. В речи «О важнейших предметах воспитания» (Казань, 1828) Лобачевский сочувственно приводит слова Ф. Бэкона: «оставьте трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на все вопросы ваши будет отвечать вам непременно и удовлетворительно». В своем сочинении «О началах геометрии», являющемся первой публикацией открытой им геометрии, Лобачевский писал: «первые понятия, с которых начинается какая-нибудь наука, должны быть ясны и приведены к самому меньшему числу. Тогда только они могут служить прочным и достаточным основанием учения. Такие понятия приобретаются чувствами; врожденным – не должно верить». Тем самым Лобачевский отвергал идею об априорном характере геометрических понятий, поддерживавшуюся И. Кантом.
Первые попытки Лобачевского доказать пятый постулат относятся к 1823 году. К 1826 году он пришел к убеждению в том, что V постулат не зависит от остальных аксиом геометрии Евклида и 11(23) февраля 1826 года сделал на заседании факультета казанского университета доклад «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных», в котором были изложены начала открытой им «воображаемой геометрии», как он называл систему, позднее получившую название неевклидовой геометрии. Доклад 1826г. вошел в состав первой публикации Лобачевского по неевклидовой геометрии – статьи «О началах геометрии», напечатанной в журнале Казанского университета «Казанский вестник» в 1829-1820гг. дальнейшему развитию и приложениям открытой им геометрии были посвящены мемуары «Воображаемая геометрия», «Применение воображаемой геометрии к некоторым интегралам» и «Новые начала геометрии с полной теорией параллельных», опубликованные в «Ученых записках» соответственно в 1835, 1836 и 1835-1838 гг. Переработанный текст «Воображаемой геометрии» появился во французском переводе в Берлине, там же в 1840г. вышли отдельной книгой на немецком языке «Геометрические исследования по теории параллельных линий» Лобачевского. Наконец, в 1855 и 1856 гг. он издал в Казани на русском и французском языках «Пангеометрию».
Высоко оценил «Геометрические исследования» Гаусс, который провел Лобачевского (1842) в члены-корреспонденты Геттингенского ученого общества, бывшего по существу Академией наук ганноверского королевства. Однако в печати в оценкой новой геометрической системы Гаусс не выступил.
Независимо от Лобачевского и гаусса к открытию неевклидовой геометрии пришел венгерский математик Янош Бояи (1802-1860), сын Ф. Бояи.
Когда Я. Бояи пришел к тем же идеям, что Лобачевский и Гаусс, отец не понял его, однако предложил напечатать краткое изложение его открытия в виде приложения к своему руководству по математике, вышедшему в 1832г. Полное название труда Я. Бояи – «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)» и его обычно коротко называют просто «Аппендикс». Открытие Я. Бояи не было признано при его жизни; Гаусс, которому Ф. Бояи послал «Аппендикс», понял его, но никак не способствовал признанию открытия Я. Бояи.
а к с и о м а
постулат в геометрии
• бесспорная, не требующая доказательств истина
• доказательство без доказательства
• исходная бездоказательность, истина, не требующая доказательств
• не требующее доказательства утверждение
• полная недоказуемость, равная полной неопровержимости. Александр Круглов
• положение, принимаемое без логического доказательства
• утверждение, которое неопровержимо, пока в нем хватает соединительной силы
• у древних греков, таких как Пифагор и Евклид, это слово означало «то, что достойно почести»
• полная недоказуемость, равная полной неопровержимости
• истина, на которую не хватило доказательств
• само собой разумеющееся
• положение, не требующее доказательств
• принятая в науке истина
• постулат в математике
• догма в математике
• положение, принимаемое без доказательств
• не требует доказательств
• положение, принимаемое без доказ.
• истиное исходное положение теории
• истинное исходное положение теории
• Истина, не требующая доказательства
• Исходное положение какой-либо теории или науки, принимаемое без доказательств
• Положение, принимаемое без доказательств
• ж. греч. очевидность, ясная по себе и бесспорная истина, не требующая доказательств, напр. целое всегда, больше части своей; основная истина, самоистина, ясноистина
• положение не требующее доказательств
• положение, принимаемое без доказ
• у древних греков, таких как Пифагор и Евклид, это слово означало «то, что достойно почести»