Последовательность фебачини что это
Фибоначчи повсюду!
Числа Фибоначчи названы в честь Леонардо Фибоначчи из города Пизы (современная Италия). На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.
Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
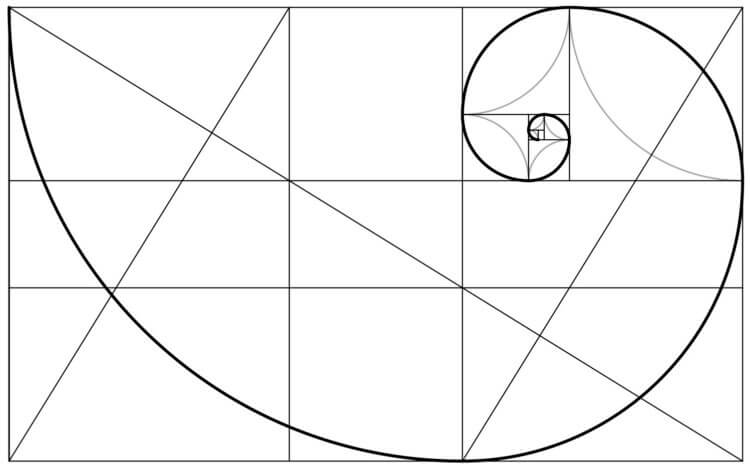
Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.
Числа Фибоначчи в природе
Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.
Числа Фибоначчи в теле человека
Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.
Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.
Числа Фибоначчи в биржевой торговле
Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.
Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.
Числа Фибоначчи в фотографии и искусстве
В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.
Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.
Может именно из-за этого Дональд Трамп был избран президентом? (шутка):
Тем не менее, никогда не стоит недооценивать скрытые силы последовательности Фибоначчи.
Золотое сечение и числа Фибоначчи
Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.
Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].
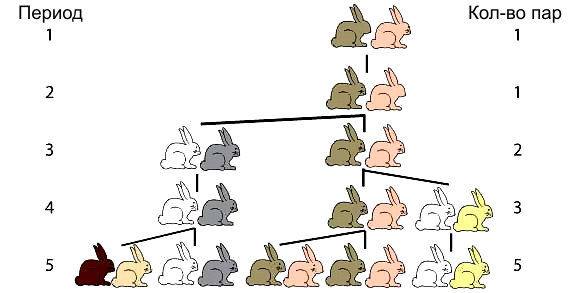
Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).
Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].
В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).
Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].
Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].
Золотые пропорции включают в себя такие моменты:
— как ширина верхнего переднего зуба относится к ширине нижнего;
— как соотносятся между собой по ширине:
2 резца в нижнем фронтальном ряду;
двое резцов в верхнем ряду;
— какое имеется расстояние между премолярами и т.д.
Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».
Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].
Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].
Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:
• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
• 2 — понимает речь и действует, пользуясь словесными указаниями;
• 3 — действует посредством слова, задаёт вопросы;
• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;
• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…
Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.
1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.
Число Фибоначчи. Почему оно так популярно в природе?
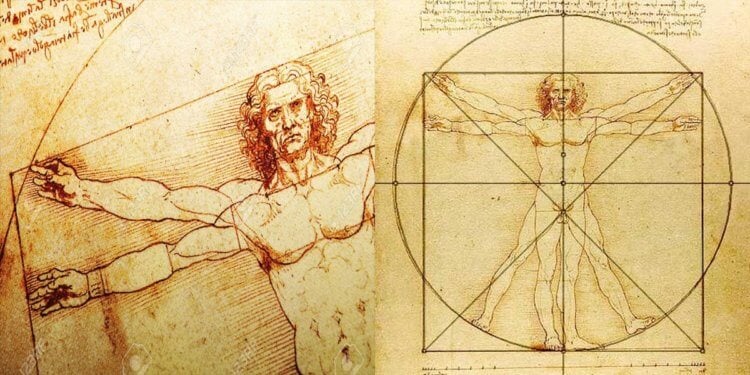
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
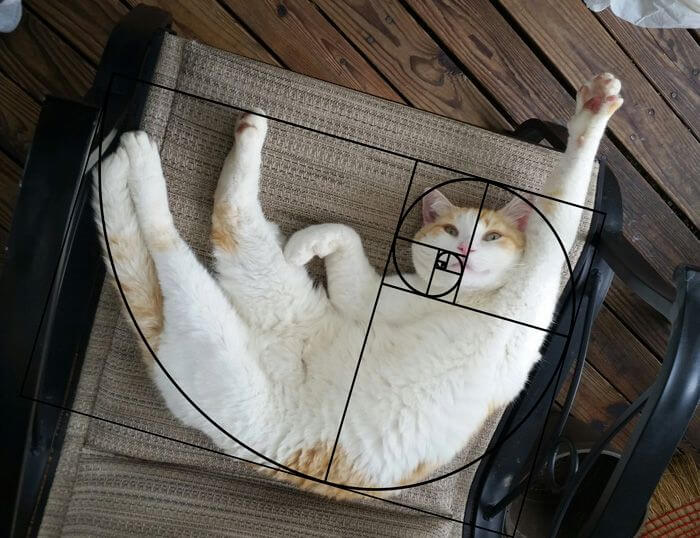
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Пару десятков лет назад вы наверняка слышали истории о том, как некоторые люди обнаруживали на полях загадочные круги. Очевидцы уверяли, что эти узоры были о…
Где все инопланетяне? Сложность в их обнаружении может заключаться в нас самих, считает группа психологов из Кадисского университета (Испания). В статье учен…
В жизни каждого человека возникали ситуации, когда обыкновенный предмет казался очень похожими на человеческое лицо или мордочку животного. Шар для боулинга …
Числа Фибоначчи — что это и для чего они нужны?
Научитесь грамотно оценивать стоимость компании не только с фундаментальной точки зрения, но и «со стороны рынка».
История чисел Фибоначчи
Леонардо Пизано, по прозвищу Фибоначчи, — итальянский математик — родился в Пизе в 1170 году. Его отец работал в торговом порту на северо-востоке Алжира и часто путешествовал.
Фибоначчи изучал математику и во время обширных путешествий познакомился с индийско-арабской системой счисления. Оттуда математик и узнал о числовой последовательности, которую в древней Индии использовали в стихосложении.
Названа последовательность в честь итальянца, потому что именно он представил ее европейскому обществу в труде «Книга абака».
Что такое числа Фибоначчи?
Числа Фибоначчи — это ряд, состоящий из целых чисел. Их особенность заключается в том, что каждый элемент представляет собой сумму двух предыдущих чисел.
Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности.
Математик обратил внимание на числовую последовательность, когда думал о разведении кроликов.
Задача была поставлена следующим образом: «Если новорожденную пару кроликов, самца и самку, поместить в поле, то сколько пар кроликов будет через год?». Но как известно, ни одну практическую задачу невозможно решить без некоторых ограничений и предположений. Поэтому, к условию задачи добавились следующие допущения:
Схема разведения кроликов выглядит следующим образом:
Так как по условию задачи в поле поместили новорожденных кроликов, то спариваться они не могут, так как не достигли половой зрелости. Через месяц кролики начинают спариваться и еще через один – рождается первая пара потомков. «Родители» продолжают наращивать потомство, а дети месяц ждут своего взросления, чтобы тоже стать родителями. В итоге, через 3 месяца по полю будут бегать три пары кроликов. Через 4 месяца уже 5 пар, а через 5 месяцев – 8.
Уже прослеживается закономерность. В конце каждого месяца количество пар кроликов будет больше, чем в предыдущем месяце ровно на столько, сколько пар было два месяца назад.
С точки зрения математики — это красивая последовательность. Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.
Это соотношение можно найти во предметах, которые нас отгружают: гармония в гранях снежинок, в расположении лепестков цветов, ячеек ананаса, завитки раковин у улитки — все подчиняется правилу золотого сечения. Даже строение нашего тела гармонично: если измерить наш рост и разделить на расстояние от пояса до ступней или длину руки на расстояние от локтя до кончиков пальцев, получится известное нам соотношение 1,618.
Научитесь грамотно оценивать стоимость компании не только с фундаментальной точки зрения, но и «со стороны рынка».
Если мы видим человека и его внешность кажется красивой, то скорее всего пропорции его лица соотносятся с соотношением чисел Фибоначчи.
Природа полагается на эту врожденную пропорцию для поддержания баланса.
Финансовые рынки имеют ту же математическую основу, что и перечисленные природные явления. Давайте рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.
Числа Фибоначчи в трейдинге
Впервые изучением графиков биржевых котировок и поиском взаимосвязей занялся Ральф Hельсон Эллиотт, американский финансист. Ему удалось обнаружить в поведении фондового рынка особую гармонию. Как вы уже догадались – гармонию золотого сечения.
Мы рассмотрим четыре инструмента технического анализа, использующих последовательность Фибоначчи, активно применяемые трейдерами – это уровни, дуги, веер и временные зоны Фибоначчи.
Сначала поговорим об уровнях коррекции.
1. Коррекции Фибоначчи
Коррекция Фибоначчи — популярный инструмент, используемый трейдерами. Еще больше об инструментах, которые используют трейдеры, можно узнать на открытом курсе «Трейдинг и личные инвестиции».
Как это работает: берутся экстремальные точки на графике акций: нижний и верхний уровни цены долгосрочного тренда, и вертикальное расстояние между ними делится на коэффициенты Фибоначчи: 23,6%, 38,2%, 50%, 61,8% и 100%. После определения уровней соотношений на графике рисуются горизонтальные линии, представляющие уровни, указывающие на возможные уровни поддержки (цена перестает идти ниже) и сопротивления (цена перестает идти выше).
Откуда берутся эти значения процентов?
Трейдеры используют уровни коррекции Фибоначчи для определения стратегических моментов для получения выгодной цены. Если тренд возрастает, то уровни коррекции Фибоначчи используются как потенциальные точки покупки при откатах, если тренд убывающий, то как точки входа для коротких продаж.
2. Дуги Фибоначчи
Дуги Фибоначчи учитывают как время, так и цену, также указывая на потенциальные области поддержки и сопротивления.
Поиск максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем рисуются три изогнутые линии, похожие на полукруги, на расстоянии 38,2%, 50% и 61,8% от желаемой точки. Полукруглые дуги показывают, где цена находит поддержку или сопротивление в будущем.
После роста цены дуги показывают до чего цена может откатиться, прежде чем снова начнет расти. После снижения цены дуги показывают, куда цена может подняться, прежде чем снова начнет падать.
3. Веера Фибоначчи
Веера Фибоначчи — это диагональные линии, образующие веер. Как и в предыдущих методах, сначала находятся максимум и минимум тренда. Если траектория возрастающая, то через точку максимума, если убывающие – через точку минимума условно проводится вертикальная линия.
Затем на линии отмечаются уровни: 38,2%, 50% и 61,8%. Дальше соединяются точки первого экстремума и точки, условно отмеченные на невидимой прямой. Получившиеся диагональные линии также указывают на области поддержки и сопротивления.
4. Временные зоны Фибоначчи
Временные зоны — это серия линий, параллельных оси ОУ, отстоящих друг от друга на расстоянии, пропорциональном элементам последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. д.).
Трейдер отмечает на графике очевидный ценовой тренд (его минимум и максимум). Расстояние между этими точками будет задавать единичный отрезок. Дальше рисуются прямые линии соответственно последовательности Фибоначчи: представьте, что вы строите график на координатной плоскости OXY. Ось OX разбита на длины единичного отрезка от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8…. и так далее.
Теперь вспомним, как выглядит ряд Фибоначчи: 0, 1, 2, 3, 5, 8…. Теперь именно в этих точках на оси OX и будут строиться вертикальные линии, соответствующие временным зонам. Каждая линия указывает время, в которое можно ожидать резкий скачок или спад цены.
Описанные инструменты далеко не единственные методы анализа графиков, использующих золоте сечение и числа Фибоначчи. Возможно, вы слышали и о таких инструментах, как клин, канал, спираль, также названных в честь Фибоначчи. Они отличаются способами построения и внешним видом, но смысл остается один — оценить области поддержки и сопротивления цены. Часто используют несколько методов одновременно для улучшения качества прогнозирования. Подробнее об инструментах, которые используются в трейдинге, можно узнать в бесплатной демо-версии книги по трейдингу.
Надеемся, вы тоже найдете собственное «нишевое» применение исследованиям Фибоначчи и добавите эти методы в свой набор инвестиционных инструментов.
Автор: Алексанян Андрон, эксперт SF Education
Научитесь грамотно оценивать стоимость компании не только с фундаментальной точки зрения, но и «со стороны рынка».