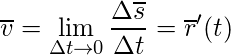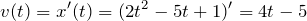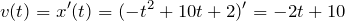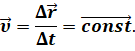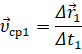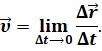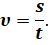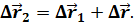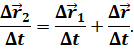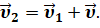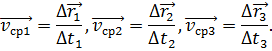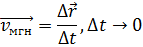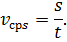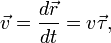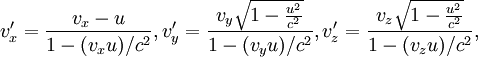Понятие мгновенная скорость вводится потому что
Мгновенная скорость движения
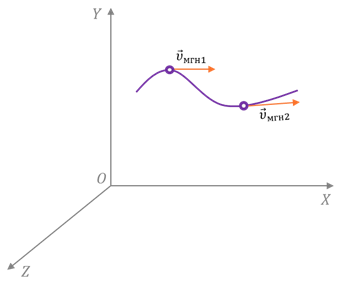
Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.
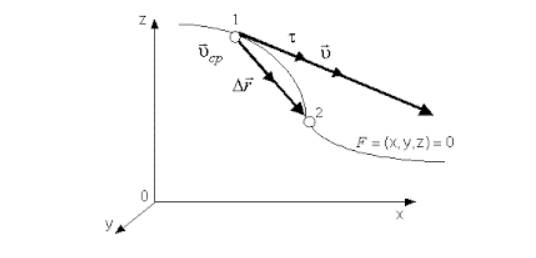
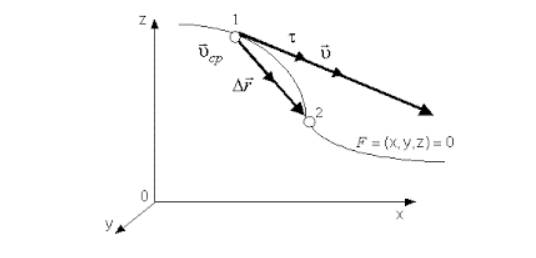
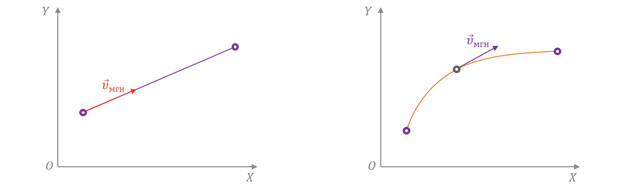
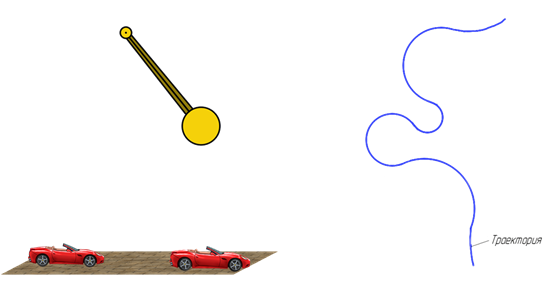
Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.
Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый 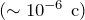
Примеры решения задач по теме «Мгновенная скорость»
| Задание | О какой скорости – средней или мгновенной – идет речь в следующих случаях: |
1) самолет летит из Санкт-Петербурга в Москву со скоростью 800 км/ч;
2) пуля вылетает из винтовки со скоростью 800 м/с;
3) велосипедист едет по шоссе со скоростью 12 км/ч;
4) прибор показывает скорость тепловоза 75 км/ч?
2) и 4) – речь идет о мгновенной скорости.
| Задание | Закон движения точки по прямой задается уравнением 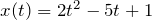 . Найти мгновенную скорость точки через 10 секунд после начала движения. . Найти мгновенную скорость точки через 10 секунд после начала движения. |
| Решение | Мгновенная скорость точки – это первая производная радиус-вектора по времени. Поэтому для мгновенной скорости можно записать: |
Через 10 секунд после начала движения мгновенная скорость будет иметь значение:
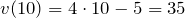
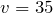 м/с.
м/с.| Задание | Тело движется по прямой так, что его координата 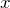 (в метрах) изменяется по закону (в метрах) изменяется по закону 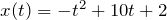 . Через сколько секунд после начала движения тело остановится? . Через сколько секунд после начала движения тело остановится? |
| Решение | Найдем мгновенную скорость тела: |
В момент остановки мгновенная скорость тела будет равна нулю:
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
Мгновенная скорость. Сложение скоростей
Урок 4. Физика 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Мгновенная скорость. Сложение скоростей»
Самым простым видом механического движения является прямолинейное движение с постоянной по модулю и направлению скоростью:
Однако не будем забывать о том, что равномерно движение — это модель реального движения. В действительности же реальные тела чаще всего движутся не равномерно. Например, все вы знаете, что автомобиль в начале своего движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине пути он, возможно, будет недолго двигаться с постоянной скоростью. А при торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля является неравномерным. Поэтому описать его с помощью уравнения движения мы не можем, так как скорость тела постоянно меняется.
Но нам на помощь приходить понятие мгновенной скорости, то есть скорости точки в данный момент времени (или в данной точке траектории).
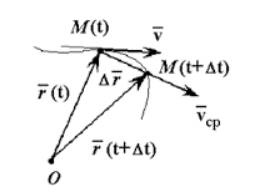
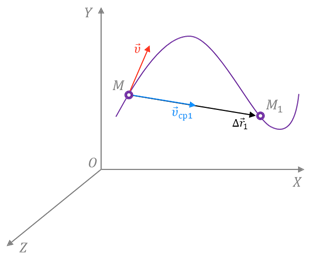
Чтобы понять, как определяется мгновенная скорость, рассмотрим неравномерное движение материальной точки по криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М. А спустя некоторый промежуток времени Δt1 — положение М1.
Укажем на рисунке перемещение, которое совершила точка за этот промежуток времени.
Если теперь мы с вами разделим это перемещение на промежуток времени, в течение которого оно произошло, то тем самым найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени. Эта скорость называется средней скоростью перемещения. Она показывает, какое перемещение в среднем совершала точка за единицу времени.
Направление этой скорости совпадает с направлением вектора перемещения точки.
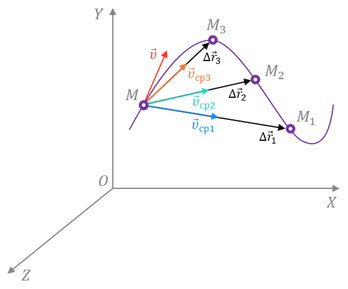
Но как же нам определить скорость точки в положении М? Давайте попробуем уменьшить рассматриваемый промежуток времени. Из рисунка видим, что в этом случае точка совершит меньшее перемещение. Средняя же скорость точки на этом участке хотя и не равна скорости в точке М, но уже ближе к ней.
Если мы продолжим уменьшать промежутки времени и, соответственно, перемещения, то очень скоро мы придём к тому, что средние скорости будут незначительно отличаться друг от друга и от скорости точки в положении М. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время. Следовательно, при стремлении промежутка времени к нулю отношение 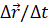
Физическая векторная величина, равная пределу отношения перемещения к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенной скоростью:
Направление вектора мгновенной скорости зависит от вида движения точки. Так, если точка движется прямолинейно, то направление мгновенной скорости совпадает с направлением движения. А вот в случае криволинейного движения вектор мгновенной скорости направлен по касательной к траектории.
В этом легко убедиться, если понаблюдать за раскалёнными частицами, отрывающимися от точильного камня. Или за частицами грязи, вылетающими из-под колеса буксующего автомобиля.
Для описания неравномерного движения точки, помимо понятия средней скорости перемещения, в физике чаще используют понятие средней путевой скорости. Она определяется отношением пути к промежутку времени, за который этот путь пройдён:
Проще говоря, средняя путевая скорость показывает, какой путь в среднем проходило тело за единицу времени.
Однако не стоит забывать о том, что средняя путевая скорость характеризует движение за весь промежуток времени в целом. Например, когда мы слышим, что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью 100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но во время движения он мог заехать на заправку, где-то двигаться с бо́льшей или меньшей скоростью. Иными словами, средняя путевая скорость не даёт информации о скорости движения точки в каждый момент времени.
Для примера давайте с вами определим среднюю путевую скорость движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а вторую — со скоростью 25 м/с.
Мы уже с вами не раз говорили о том, что характер движения точки зависит от того, относительно каких тел мы рассматриваем это движение (то есть от выбора системы отсчёта). Но так как тело отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же тела можно одновременно рассматривать в разных системах координат.
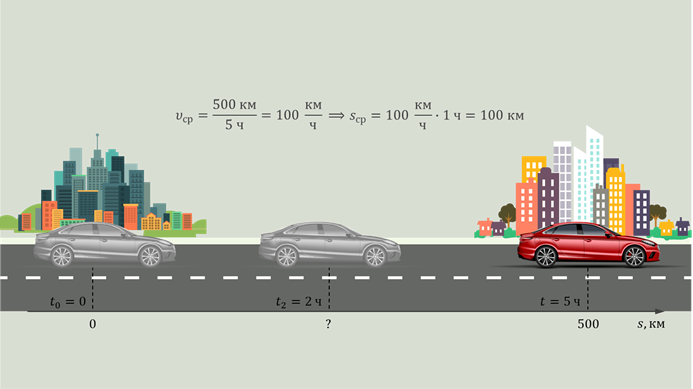
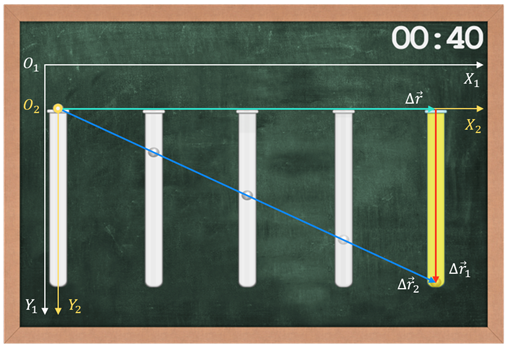
Рассмотрим такой опыт. Пусть у нас есть стеклянная трубка, заполненная вязкой жидкостью. Опустим в неё тяжёлый шарик и будем перемещать трубку относительно школьной доски в горизонтальном направлении, не меняя ориентации трубки. Одновременно будем наблюдать за движением шарика и отмечать его положения через равные интервалы времени.
Теперь выберем две системы координат: одну свяжем с доской и назовём неподвижной, а вторую — с трубкой и назовём движущейся.
Из рисунка видно, что перемещение точки относительно неподвижной системы отсчёта равно векторной сумме её перемещения относительно движущейся системы и перемещения движущейся системы отсчёта относительно неподвижной:
В этом состоит принцип независимости движений.
Теперь разделим записанное нами уравнение на промежуток времени, в течение которого произошли эти перемещения:
И учтём, что отношения перемещений к промежутку времени равны скоростям:
Таким образом получаем, что скорость тела относительно неподвижной системы отсчёта равна векторной сумме его скорости относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.
Данное утверждение называется законом сложения скоросте́й Галилея. Он справедлив как для равномерного, так и для неравномерного движения. Только в этом случае складываются мгновенные скорости.
Однако этот закон нельзя применять для точек, движение которых происходит со скоростями, близкими к скорости света в вакууме.
Для примера решим такую задачу. На какой угол следует отклонится от перпендикуляра к течению реки и сколько времени нужно плыть на лодке, чтобы пересечь реку перпендикулярно её течению, если скорость лодки относительно воды 3 м/с, скорость течения реки — 1,5 м/с, а ширина русла — 400 м?
Неравномерное движение. Мгновенная скорость
Урок 6. Физика 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Неравномерное движение. Мгновенная скорость»
Ранее мы рассматривали равномерное прямолинейное движение. Строго говоря, такое движение — это идеализированный пример. На самом деле тела двигаются неравномерно. Например, автомобиль едет чуть быстрее или чуть медленнее в определённые промежутки времени.
Да и траектория его никогда не является прямой на достаточно длинных участках.
Существует также колебательное движение, примером которого может являться движение маятника. Кроме того, как вы знаете, тело, находящееся в свободном падении, двигается с ускорением. Наконец, тело, двигающееся по кривой, обладает центростремительным ускорением. Все эти примеры являются примерами неравномерного движения. Неравномерным движением называется такое движение, при котором расстояния, пройденные за одинаковые промежутки времени, не равны.
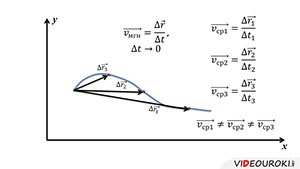
Именно, с неравномерным движением связано понятие мгновенной скорости. Чтобы понять, что такое мгновенная скорость, рассмотрим простой пример. На рисунке вы видите траекторию, по которой перемещается точка.
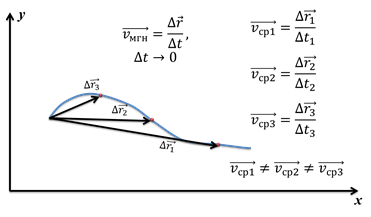
Отметим три случайных положения этой точки на траектории. Тогда мы можем найти три разных вектора перемещения: 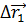
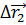
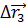
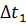
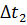
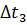
Очевидно, что эти скорости будут неравны. Но по мере уменьшения промежутка времени, средние скорости всё меньше и меньше будут отличаться друг от друга. В конце концов, если мы возьмём бесконечно малый промежуток времени, выражение
будет стремиться к определённому значению. То есть, это скорость в данный момент времени или, точнее сказать, мгновенная скорость.
Заметим, что какой бы сложной ни была траектория движения, если мы возьмём бесконечно малый промежуток времени, то на нём перемещение будет казаться прямолинейным. В этом случае, мы можем подсчитать скорость по формуле для прямолинейного движения. Но в каждое последующее мгновение, скорость будет меняться. Именно поэтому, она и называется мгновенной скоростью.
Мгновенная скорость — это величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
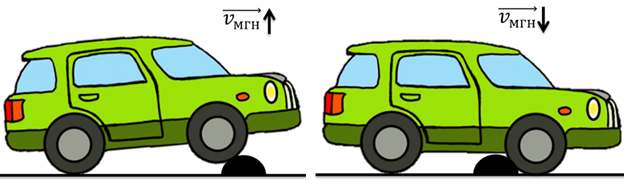
Мгновенная скорость направлена по касательной к траектории. Например, если вы едете в машине и наехали на кочку, то вас подбрасывает вверх. Почему? Потому что в тот миг, когда машина переезжает через кочку, мгновенная скорость направлена вверх. Но в следующее же мгновение, она направлена вниз, а еще через мгновение, скорость снова направлена также, как и была направлена до кочки.
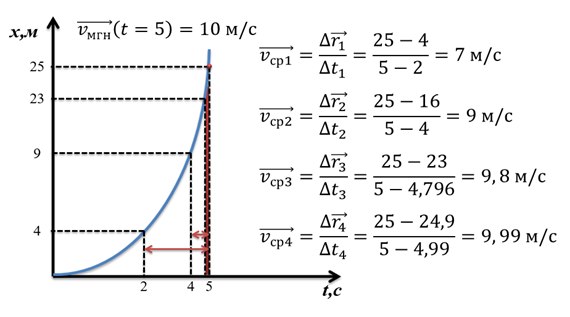
Рассмотрим конкретный пример. Вы видите график зависимости положения материальной точки от времени при равноускоренном движении.
График представляет собой параболу. Очевидно, что в каждой точке скорость разная. Если мы рассчитаем среднюю скорость в период от 2 до 5 секунд, то она будет равна 7 м/с. Рассмотрим теперь промежуток времени от 4 до 5 секунд. В этом случае, средняя скорость будет равна 9 м/с. Рассмотрим теперь участок от 4,796 секунд до 5 секунд. Этот промежуток времени довольно мал, поэтому если мы достаточно приблизим график, то траектория будет казаться почти прямой. Средняя скорость на этом участке равна 9,8 м/с.
Как видите, с уменьшением интервала времени, средняя скорость стремится к какому-то определённому значению. То есть, к значению мгновенной скорости в момент времени t = 5 с, которое в нашем случае равно 10 м/с. Если мы подсчитаем среднюю скорость на временном интервале, равным 0,01 с, то убедимся, что средняя скорость почти равна 10 м/с.
Заметим, что во всех упомянутых примерах мы рассматривали среднюю скорость перемещения. Существует также, такое понятие, как средняя путевая скорость. Именно путевая скорость чаще всего используется для описания движения.
Средняя путевая скорость определяется отношением пройденного пути к промежутку времени, за который этот путь пройден:
Мы уже говорили, что пройденный путь всегда больше либо равен модулю перемещения. Из этого можно сделать вывод, что средняя путевая скорость больше либо равна модулю средней скорости перемещения:
Мгновенная скорость
Ско́рость (часто обозначается 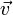
В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).
Содержание
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 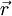
Здесь v — модуль скорости, 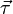
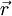
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Мгновенная и средняя скорость
Преобразование скорости
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна 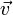

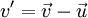
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость 
Единицы измерения скорости
Соотношение между единицами скорости
См. также
Полезное
Смотреть что такое «Мгновенная скорость» в других словарях:
мгновенная скорость — скорость; мгновенная скорость Скорость точки жидкости, рассматриваемая как векторная функция переменных Эйлера … Политехнический терминологический толковый словарь
мгновенная скорость — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN instantaneous speedinstantaneous velocity … Справочник технического переводчика
мгновенная скорость — akimirkinis greitis statusas T sritis automatika atitikmenys: angl. instantaneous speed vok. augenblickliche Geschwindigkeit, f; momentane Geschwindigkeit, f; Momentangeschwindigkeit, f rus. мгновенная скорость, f pranc. vitesse instantanée, f… … Automatikos terminų žodynas
мгновенная скорость — akimirkinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Greitis tam tikrą akimirką. atitikmenys: angl. instantaneous speed; instantaneous velocity vok. augenblickliche Geschwindigkeit, f; Momentangeschwindigkeit, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
мгновенная скорость — akimirkinis greitis statusas T sritis fizika atitikmenys: angl. instantaneous velocity vok. augenblickliche Geschwindigkeit, f; Momentangeschwindigkeit, f rus. мгновенная скорость, f pranc. vitesse instantanée, f … Fizikos terminų žodynas
МГНОВЕННАЯ СКОРОСТЬ РОСТА ПОПУЛЯЦИИ — скорость изменения числа организмов r в зависимости от времени в данный момент. Определяется по формуле: ║ где dN изменение числа организмов в данный момент времени dt; N число особей в популяции. См. также Мальтузианский параметр.… … Экологический словарь
мгновенная скорость фильтрования — Скорость фильтрования в данный момент времени. [ГОСТ 16887 71] Тематики фильтрование, центрифугирование, сепарирование … Справочник технического переводчика
мгновенная скорость ветра — 3.7 мгновенная скорость ветра: Скорость ветра в выделенной точке пространства скорость, которую имеет бесконечно малый объем воздуха, окружающий данную точку, характеризуется модулем и направлением. Источник: ГОСТ Р 54433 2011: Возобновляемая… … Словарь-справочник терминов нормативно-технической документации
Мгновенная скорость фильтрования — 57. Мгновенная скорость фильтрования Скорость фильтрования в данный момент времени Источник: ГОСТ 16887 71: Разделение жидких неоднородных систем методами фильтрования и центрифугирования. Термины и определения … Словарь-справочник терминов нормативно-технической документации
мгновенная скорость нагрева — Syn: мгновенная скорость нагревания … Металлургический словарь терминов