Пользуясь рисунком 18 а докажите что проекция вектора

§ 7. Перемещение тела при прямолинейном равноускоренном движении

Выведем формулу, с помощью которой можно рассчитать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к рисунку 14. Как на рисунке 14, (а), так и на рисунке 14, (б) отрезок АС представляет собой график проекции вектора скорости тела, движущегося с постоянным ускорением а (при начальной скорости 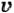₀).

Напомним, что при прямолинейном равномерном движении тела проекция вектора перемещения, совершённого этим телом, определается по той же формуле, что и площадь прямоугольника, заключённого под графиком проекции вектора скорости (см. рис. 6). Поэтому проекция вектора перемещения численно равна площади этого прямоугольника.

Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения sx можно определять по той же формуле, что и площадь фигуры, заключённой между графиком АС, осью Ot и отрезками ОА и ВС, т. е. что и в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Ot (см. рис. 14, а) выделим маленький промежуток времени db. Из точек d u b проведём перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках а и с.

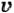
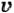
Таким образом, за промежуток времени, соответствующий отрезку db, скорость тела меняется от _ax до _cx.

За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно. Поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т. е. от движения с постоянной скоростью.

В этом случае участок ас графика можно считать горизонтальным, а полоску acbd — прямоугольником. Значит, площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку db.

На такие полоски можно разбить всю площадь фигуры ОАСВ, являющейся трапецией. Следовательно, проекция вектора перемещения s_x за промежуток времени, соответствующий отрезку ОВ, численно равна площади S трапеции ОАСВ и определяется по той же формуле, что и эта площадь.

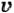
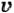
Согласно правилу, приведённому в школьных курсах геометрии, площадь трапеции равна произведению полусуммы её оснований на высоту. Из рисунка 14, (б) видно, что основаниями трапеции ОАСВ являются отрезки ОА = _0x и ВС = _x, а высотой — отрезок ОВ = t. Следовательно,

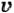
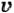
Поскольку _x = _0х + a_xt, a S — s_x, то можно записать:

Таким образом, мы получили формулу для расчёта проекции вектора перемещения при равноускоренном движении.

По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью, только в этом случае векторы скорости и ускорения будут направлены в противоположные стороны, поэтому их проекции будут иметь разные знаки.

Вопросы

1. Пользуясь рисунком 14, а, докажите, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ.
2. Запишите уравнение для определения проекции вектора перемещения тела при его прямолинейном равноускоренном движении.

Упражнение 7

2. Поезд, идущий со скоростью 15 м/с, остановился через 20 с после начала торможения. Считая, что торможение происходило с постоянным ускорением, определите перемещение поезда за 20 с.

3. *1 Приведите формулу к виду При необходимости воспользуйтесь указаниями в ответах.

1 Звёздочкой обозначены задачи повышенной сложности.

Источник

Вопросы.

1. Пользуясь рисунком 14, а, докажите, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ.

2. Запишите уравнение для определения проекции вектора перемещения тела при его прямолинейном равноускоренном движении.

2. Поезд, идущий со скоростью 15 м/с, остановился через 20 с после начала торможения. Считая, что торможение происходило с постоянным ускорением, определите перемещение поезда за 20 с.

3. Приведите формулу (1) из § 7 к виду . При необходимости воспользуйтесь указаниями в ответах.

Источник

Пользуясь рисунком 18 а докажите что проекция вектора

1.Как доказать, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ?

При прямолинейном равномерном движении проекция вектора перемещения, совершенного телом, определяется по той же формуле, что и площадь прямоугольника, заключенного под графиком проекции вектора скорости.
Поэтому проекция вектора перемещения численно равна площади этого прямоугольника.

Докажем, что и в случае прямолинейного равноускоренного движения проекцию sx вектора перемещения можно определять по той же формуле, что и площадь фигуры, заключенной под графиком скорости (АС).

За промежуток времени db скорость тела меняется от Vах до Vcх.
За этот малый промежуток времени проекция вектора скорости меняется очень незначительно.
Поэтому движение тела на этом промежутке времени мало отличается от равномерного.
Тогда участок ас графика можно считать горизонтальным, а полоску acbd — прямоугольником.
Значит, площадь этой полоски численно равна проекции вектора перемещения за время db.

На такие полоски можно разбить всю площадь фигуры ОАСВ, являющейся трапецией.
Тогда проекция sx вектора перемещения за времени, равное ОВ, численно равна площади трапеции ОАСВ и определяется по той же формуле, что и эта площадь.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Основаниями трапеции ОАСВ являются отрезки OA = V_ox и ВС = V_х, а высота равна ОВ = t.
Тогда:

Так как :

Получаем:

2. Как выглядит формула для определения проекции вектора перемещения тела при его прямолинейном равноускоренном движении?

Формула для расчёта проекции вектора перемещения при равноускоренном движении:

По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью (при торможении тела), только в этом случае векторы скорости и ускорения будут направлены в противоположные стороны, поэтому их проекции будут иметь разные знаки.

Источник

§ 7. Перемещение тела при прямолинейном равноускоренном движении

Выведем формулу, с помощью которой можно рассчитать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к рисунку 14. Как на рисунке 14, а, так и на рисунке 14, б отрезок АС представляет собой график проекции вектора скорости тела, движущегося с постоянным ускорением а (при начальной скорости v₀).

Рис. 14. Проекция вектора перемещения тела, движущегося прямолинейно и равноускоренно, численно равна площади S под графиком

Напомним, что при прямолинейном равномерном движении тела проекция вектора перемещения, совершенного этим телом, определяется по той же формуле, что и площадь прямоугольника, заключённого под графиком проекции вектора скорости (см. рис. 6). Поэтому проекция вектора перемещения численно равна площади этого прямоугольника.

Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения s_x можно определять по той же формуле, что и площадь фигуры, заключённой между графиком АС, осью Ot и отрезками ОА и ВС, т. е. что и в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Ot (см. рис. 14, а) выделим маленький промежуток времени db. Из точек d и b проведём перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках а и с.

Таким образом, за промежуток времени, соответствующий отрезку db, скорость тела меняется от v_ах до v_cx.

За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно. Поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т. е. от движения с постоянной скоростью.

В этом случае участок ас графика можно считать горизонтальным, а полоску acbd — прямоугольником. Значит, площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку db.

На такие полоски можно разбить всю площадь фигуры ОАСВ, являющейся трапецией. Следовательно, проекция вектора перемещения sx за промежуток времени, соответствующий отрезку ОВ, численно равна площади S трапеции ОАСВ и определяется по той же формуле, что и эта площадь.

Согласно правилу, приведённому в школьных курсах геометрии, площадь трапеции равна произведению полусуммы её оснований на высоту. Из рисунка 14, б видно, что основаниями трапеции ОАСВ являются отрезки ОА = v_0x и ВС = v_x, а высотой — отрезок OB = t. Следовательно,

Поскольку v_x = v_0x + a_xt, a S = s_x, то можно записать:

Таким образом, мы получили формулу для расчёта проекции вектора перемещения при равноускоренном движении.

По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью, только в этом случае векторы скорости и ускорения будут направлены в противоположные стороны, поэтому их проекции будут иметь разные знаки.

Вопросы

Упражнение 7

При необходимости воспользуйтесь указаниями в ответах.

Источник

9 класс

§ 7. Перемещение тела при прямолинейном равноускоренном движении

Выведем формулу, с помощью которой можно рассчитать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к рисунку 14. Как на рисунке 14, а, так и на рисунке 14, б отрезок AC представляет собой график проекции вектора скорости тела, движущегося с постоянным ускорением α (при начальной скорости υ₀).

Напомним, что при прямолинейном равномерном движении тела проекция вектора перемещения, совершённого этим телом, определяется по той же формуле, что и площадь прямоугольника, заключённого под графиком проекции вектора скорости (см. рис. 6).

Поэтому проекция вектора перемещения численно равна площади этого прямоугольника.

Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения s_x можно определять по той же формуле, что и площадь фигуры, заключённой между графиком АС, осью Ot и отрезками OA и ВС, т. е. что и в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Ot (см. рис. 14, а) выделим маленький промежуток времени db. Из точек d и b проведём перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках а и с.

Таким образом, за промежуток времени, соответствующий отрезку db, скорость тела меняется от υ_ax до υ_cx.

За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно. Поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т. е. от движения с постоянной скоростью.

В этом случае участок ас графика можно считать горизонтальным, а полоску acbd — прямоугольником. Значит, площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку db.

На такие полоски можно разбить всю площадь фигуры OACB, являющейся трапецией. Следовательно, проекция вектора перемещения sx за промежуток времени, соответствующий отрезку OB, численно равна площади S трапеции OACB и определяется по той же формуле, что и эта площадь.

Согласно правилу, приведённому в школьных курсах геометрии, площадь трапеции равна произведению полусуммы её оснований на высоту. Из рисунка 14, б видно, что основаниями трапеции OACB являются отрезки OA = υ_0x и BC = υx, а высотой — отрезок OB = t. Следовательно,

Поскольку υ_x = υ_0x + a_xt, a S = s_x, то можно записать:

Таким образом, мы получили формулу для расчёта проекции вектора перемещения при равноускоренном движении.

По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью, только в этом случае векторы скорости и ускорения будут направлены в противоположные стороны, поэтому их проекции будут иметь разные знаки.

Вопросы:

1. Пользуясь рисунком 14, а, докажите, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры OACB.

2. Запишите уравнение для определения проекции вектора перемещения тела при его прямолинейном равноускоренном движении.

Упражнения:

Упражнение № 7

2. Поезд, идущий со скоростью 15 м/с, остановился через 20 с после начала торможения. Считая, что торможение происходило с постоянным ускорением, определите перемещение поезда за 20 с.

3*. Приведите формулу к виду . При необходимости воспользуйтесь указаниями в ответах.

* Звёздочкой обозначены задачи повышенной сложности.

Источник