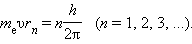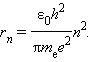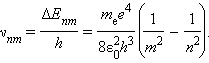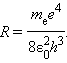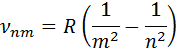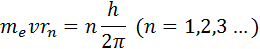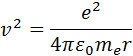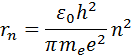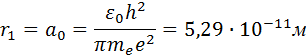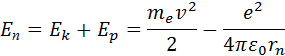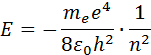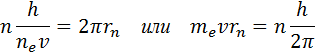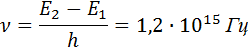Покажите что в атоме водорода на круговой стационарной боровской орбите укладывается

«Водородоподобный атом»

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

к решению задач по атомной физике

Ответственный редактор канд. физ.-мат. наук

Компьютерный набор и верстка инженер

Печатается в соответствии с решением кафедры общей физики физического факультета РГУ, протокол № 21 от 25 апреля 2006 г.

1.Первый постулат Бора (условие стационарности орбит):

Из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные орбиты (стационарные состояния), для которых момент импульса электрона удовлетворяет следующему условию:

,

где m–масса электрона, v – скорость электрона на орбите радиуса r, n – номер орбиты (главное квантовое число n=1,2,3..), – постоянная Планка.

Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, не излучает электромагнитных волн.

2. Второй постулат Бора

При переходе атома из стационарного состояния с большей энергией Ei в стационарное состояние с меньшей энергией Ej происходит излучение кванта света (фотона) с энергией :

,

где w – циклическая частота излучения при переходе с i-ой на j-ю орбиту (i>j), Ei и Ej — энергии электрона на этих орбитах.

Такое же соотношение выполняется и в случае поглощения фотона, когда атом переходитс низшего энергетического уровня Ej на более высокий уровень Ei.

3. Обобщенная формула Бальмера:

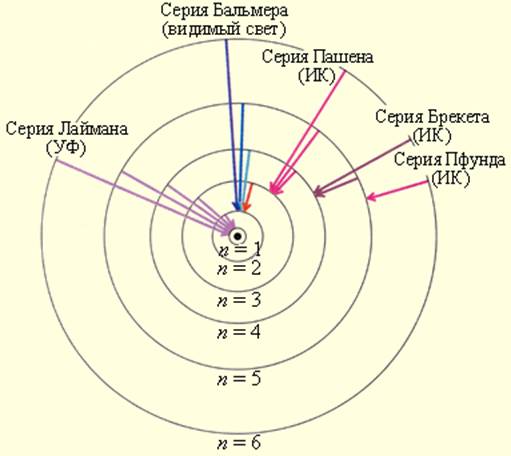
Излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий, причем они расположены не беспорядочно, а объединяются в группы или, как их называют, серии линий. Было обнаружено, что частоты волн в различных сериях, описываются следующей формулой – формулой Бальмера:

где ,

где w – циклическая частота перехода между состояниями с квантовыми числами n1 и n2, R – постоянная Ридберга, Z – заряд ядра (в единицах е), k = 1/4peo, eo – диэлектрическая постоянная, ( n1=1 – серия Лаймана, n1 =2 – серия Бальмера, n1=3 – серия Пашена, n1=4 – серия Брэкета, n1=5 – серия Пфунда, n1=6 – серия Хэмфри).

Серия Лаймана находится в ультрафиолетовой части спектра, видимой части спектра принадлежит серия Бальмера, остальные серии лежат в инфракрасной области.

В классической электродинамике показывается, что электрон, движущийся с ускорением a, излучает в единицу времени энергию , где k=1/4pe0. Оценить на основе классических представлений «время жизни» атома, считая, что полное ускорение совпадает с центростремительным.

Для простоты будем считать, что электрон в любой момент времени, до падения на ядро, движется равномерно, по круговой орбите. Причем будем считать, что в момент времени t=0 электрон движется по первой боровской орбите, т. е. r1=0.53×10-10м. Тогда согласно 2-му Закону Ньютона

.

Тогда кинетическая энергия электрона K и ускорение а будут равны

, (1)

и полная энергия электрона в поле ядра

. (2)

или .

Подставляя в формулу (3), выражения для полной энергии Е (2) и ускорения а (1), получим

. (3)

Разделяя переменные, получим

.

Проинтегрируем это уравнение: левую часть по r от r1 до 0, а правую по t от 0 до t.

.

В результате получим

.

Подставляя в последнее выражение численные значения, получим t = 1.3×10-11с.

Если потенциальное поле обладает сферической симметрией, то

. (4)

Исходя из второго закона Ньютона

. (5)

Согласно правилу квантования Бора

Выражая из (6) скорость частицы v и подставляя в (5) найдем возможные значения r:

.

Возможные значения полной энергии будут описываться следующим уравнением:

.

Определить для водородоподобного иона радиус n-ой боровской орбиты и скорость электрона на ней. Вычислить эти величины для первой боровской орбиты атома водорода и ионов Не+ и Li++.

Поскольку электрон двигается по круговой орбите, то

, , (7)

где rn – радиус n – ой орбиты, vn – скорость электрона на n – ой орбите.

Согласно правилу квантования Бора

. (8)

Откуда . Подставляя выражение, полученное для vn в (7), получим

. (9)

Подставив (9) в (8), получим выражение для vn

.

Значения радиуса первой боровской орбиты r1 и скорости электрона на ней v1, для атомов водорода и ионов Не+ и Li++, приведены в таблице 1.

Источник

Покажите что в атоме водорода на круговой стационарной боровской орбите укладывается

Правило квантования, приводящее к согласующимся с опытом значениям энергий стационарных состояний атома водорода, Бором было угадано. Он предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде

Здесь _e – масса электрона, υ – его скорость, – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением

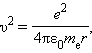где – элементарный заряд, – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением

Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией на другую стационарную орбиту с энергией атом испускает квант света, частота которого равна :

Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную равной

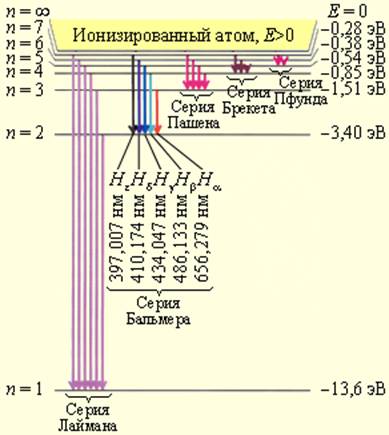
На рис. 6.3.2. изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям.

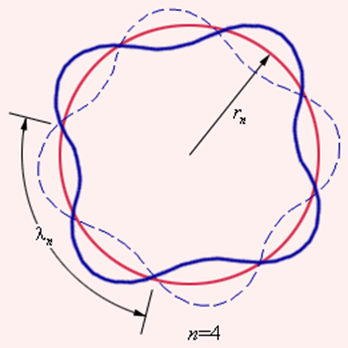
Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Однако попытки применить эту теорию к более сложным атомам не увенчались успехом. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на основе представлений о волновых свойствах частиц. Де Бройль предложил, что каждая орбита в атоме водорода соответствует волне, распространяющейся по окружности около ядра атома. Стационарная орбита возникает в том случае, когда волна непрерывно повторяет себя после каждого оборота вокруг ядра. Другими словами, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Это явление очень похоже на стационарную картину стоячих волн в струне с закрепленными концами.

В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ, т. е.

Таким образом, боровское правило квантования связано с волновыми свойствами электронов.

Согласно боровской концепции, при обратном самопроизвольном переходе атома ртуть должна испускать кванты с частотой

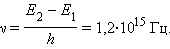Спектральная линия с такой частотой действительно была обнаружена в ультрафиолетовой части спектра излучения атомов ртути.

Представление о дискретных состояниях противоречит классической физике. Поэтому возник вопрос, не опровергает ли квантовая теория ее законы.

Половинчатая, полуклассическая теория Бора явилась важным этапом в развитии квантовых представлений, введение которых в физику требовало кардинальной перестройки механики и электродинамики. Такая перестройка была осуществлена в 20-е – 30-е годы XX века.

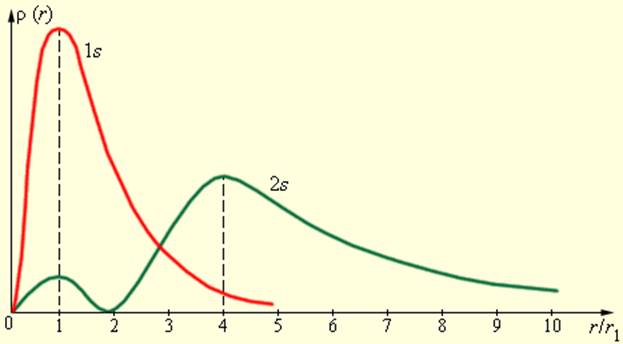
На рис. 6.3.4 изображены кривые распределения вероятности обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1 и 2.

Как видно из рис. 6.3.4, электрон в состоянии 1 (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу первой боровской орбиты. Вероятность обнаружения электрона в состоянии 2 максимальна на расстоянии от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.

Источник

Покажите что в атоме водорода на круговой стационарной боровской орбите укладывается

Квантование электронных орбит

Правило квантования орбит по Бору получило наглядную интерпретацию в теории французского физика де Бройля, высказавшего гипотезу о наличии у электрона волновых свойств (1924 г.). Согласно де Бройлю электрону (и любому другому микрообъекту) массой m, соответствует волновой процесс с длиной волны:

В применении к орбитальному движению электрона в атоме водорода на стационарной орбите, из правила квантования Бора вытекает соотношение:

Это означает, что в атоме водорода длина волны де Бройля целое число раз укладывается на длине стационарной круговой орбиты электрона.

Для атома водорода: rn = n2 r1, где r1 = 5×10–11 м – радиус первой боровской орбиты.

Таким образом, третий постулат Бора эквивалентен утверждению о существовании стоячих электронных волн на стационарных круговых орбитах.

Следует отметить, что представление о движении электрона в атоме по законам классической механики по избранным (стационарным) орбитам имеет лишь историческое значение. Современная квантовая физика описывает состояние электрона в атоме

с помощью так называемых волновых функций и отказывается

от классических представлений о траекториях движения микро-объектов.

Задачи для самостоятельного решения

В программе можно переходить на вторую, третью и четвертую стационарные круговые орбиты. При этом по длине окружности орбиты автоматически укладывается целое число (n) длин волны де Бройля.

Задача 1. Проведите компьютерный эксперимент. Убедитесь, что только при определенных значениях rn по окружности данной орбиты укладывается соответствующее число длин волн де Бройля. (Для этого нужно, при заданном n, менять радиус орбиты от

1 нм до 5 нм.) Подсчитайте число волн на каждой орбите. Как располагается волна на первой орбите?

Задача 2. Найти длины волн де Бройля для электрона, находящегося на второй, третьей и четвертой боровской орбите соответственно.

Задача 3. Используя решения предыдущей задачи, найти импульс и скорость электрона на каждой орбите.

Задача 4. Найдите кинетическую и потенциальную энергии электрона на соответствующих орбитах. Как они изменяются с увеличением радиуса орбиты? (Для решения этой задачи используйте значения полной энергии электрона на соответствующей орбите, которые приведены в разделе «Постулаты Бора».)

Задача 5. На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 0,5 мкм?

Источник

Атом водорода. Линейчатые спектры

Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко времени создания теории он был хорошо изучен экспериментально. Было известно, что он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона, а масса в 1836 раз превышает массу электрона. Еще в начале XIX века были открыты дискретные спектральные линии в видимой области излучения атома водорода (так называемый линейчатый спектр). Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно (И. Бальмер, 1885 г.). Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Позже аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра. В 1890 году Йоханнес Ридберг получил эмпирическую формулу для частот спектральных линий:

Постулаты Бора определили направление развития новой науки – квантовой физики атома. Но они не содержали рецепта определения параметров стационарных состояний (орбит) и соответствующих им значений энергии En.

Правило квантования, приводящее к согласующимся с опытом значениям энергий стационарных состояний атома водорода, Бором было угадано. Он предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде

Здесь m_e – масса электрона, υ – его скорость, rn – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса r в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением

где e – элементарный заряд, ε₀ – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты rn связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением

Самой близкой к ядру орбите соответствует значение n = 1. Радиус первой орбиты, который называется боровским радиусом, равен

Полная механическая энергия E системы из атомного ядра и электрона, обращающегося по стационарной круговой орбите радиусом rn, равна

Целое число n = 1, 2, 3, … называется в квантовой физике атома главным квантовым числом.

Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em 15 Гц,

который очень хорошо согласуется с эмпирическим значением R. Рис. 6.3.1 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

Стационарные орбиты атома водорода и образование спектральных серий

На рис. 6.3.2. изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям.

Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие различным спектральным сериям. Для первых пяти линий серии Бальмера в видимой части спектра указаны длины волн

Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Однако попытки применить эту теорию к более сложным атомам не увенчались успехом. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на основе представлений о волновых свойствах частиц. Де Бройль предложил, что каждая орбита в атоме водорода соответствует волне, распространяющейся по окружности около ядра атома. Стационарная орбита возникает в том случае, когда волна непрерывно повторяет себя после каждого оборота вокруг ядра. Другими словами, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Это явление очень похоже на стационарную картину стоячих волн в струне с закрепленными концами.

Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n = 4

В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ, т. е.

Подставляя в это соотношение длину волны де Бройля λ = h / p, где p = m_eυ – импульс электрона, получим:

Таким образом, боровское правило квантования связано с волновыми свойствами электронов.

Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были поразительны. Стало ясно, что атомы – это квантовые системы, а энергетические уровни стационарных состояний атомов дискретны. Почти одновременно с созданием теории Бора было получено прямое экспериментальное доказательство существования стационарных состояний атома и квантования энергии. Дискретность энергетических состояний атома была продемонстрирована в 1913 г., в опыте Д. Франка и Г. Герца, в котором исследовалось столкновение электронов с атомами ртути. Оказалось, что если энергия электронов меньше 4,9 эВ, то их столкновение с атомами ртути происходит по закону абсолютно упругого удара. Если же энергия электронов равна 4,9 эВ, то столкновение с атомами ртути приобретает характер неупругого удара, т. е. в результате столкновения с неподвижными атомами ртути электроны полностью теряют свою кинетическую энергию. Это означает, то атомы ртути поглощают энергию электрона и переходят из основного состояния в первое возбужденное состояние,

Согласно боровской концепции, при обратном самопроизвольном переходе атома ртуть должна испускать кванты с частотой

Спектральная линия с такой частотой действительно была обнаружена в ультрафиолетовой части спектра излучения атомов ртути.

Представление о дискретных состояниях противоречит классической физике. Поэтому возник вопрос, не опровергает ли квантовая теория ее законы.

Квантовая физика не отменила фундаментальных классических законов сохранения энергии, импульса, электрического разряда и т. д. Согласно сформулированному Н. Бором принципу соответствия, квантовая физика включает в себя законы классической физики, и при определенных условиях можно обнаружить плавный переход от квантовых представлений к классическим. Это можно видеть на примере энергетического спектра атома водорода (рис. 6.3.2). При больших квантовых числах n >> 1 дискретные уровни постепенно сближаются, и возникает плавный переход в область непрерывного спектра, вытекающего из классической физики.

Половинчатая, полуклассическая теория Бора явилась важным этапом в развитии квантовых представлений, введение которых в физику требовало кардинальной перестройки механики и электродинамики. Такая перестройка была осуществлена в 20-е – 30-е годы XX века.

Состояния, в которых орбитальное квантовое число l = 0, описываются сферически симметричными распределениями вероятности. Они называются s-состояниями (1s, 2s, …, ns, …). При значениях l > 0 сферическая симметрия электронного облака нарушается. Состояния с l = 1 называются p-состояниями, с l = 2 – d-состояниями и т. д.

На рис. 6.3.4 изображены кривые распределения вероятности ρ (r) = 4πr 2 |Ψ| 2 обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1s и 2s.

Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r₁ = 5,29·10 –11 м – радиус первой боровской орбиты

Как видно из рис. 6.3.4, электрон в состоянии 1s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу r₁ первой боровской орбиты. Вероятность обнаружения электрона в состоянии 2s максимальна на расстоянии r = 4r₁ от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.

Источник