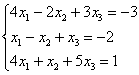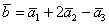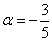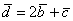Показать что векторы образуют базис и найти координаты вектора
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и н
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и найти координаты вектора d в этом базисе.
Все ответы
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и найти координаты вектора d в этом базисе.
Прямой ход метода Гаусса закончился, приступаем к обратному ходу.
Выбираем за ведущий элемент \(a_ <33>=1\),
умножим третью строку на 9 и сложим со второй строкой
$$= \left(\begin
Разделим строку 2 на 4, получаем
$$= \left(\begin
чтобы получить единичную матрицу осталось вычесть из первой строки вторую, умноженную на 5
$$= \left(\begin
и вычесть из первой строки третью строку, умноженную на 2
$$= \left(\begin
Ответ: координаты вектора \(d\) в базисе \((a;b;c)\) \(x =\left(\begin
Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
Даны векторы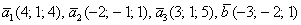 
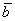
. Показать, что векторы 
образуют базис трехмерного пространства и найти координаты вектора 
в этом базисе.
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
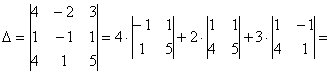
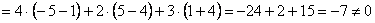
! Важно: координаты векторов обязательно записываем в столбцыопределителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Теперь вспомним теоретическую часть: если векторы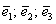 
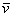
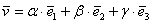
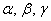
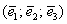
образуют базис, то любой вектор 
можно единственным способом разложить по данному базису: 
, где 
– координаты вектора в базисе 
.
Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор 
можно единственным образом разложить по данному базису:
, где 
– координаты вектора в базисе 
.
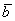
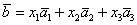
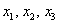
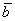
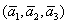
По условию и требуется найти координаты .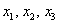
Для удобства объяснения поменяю части местами: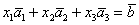 
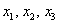
. В целях нахождения следует расписать данное равенство покоординатно: 
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя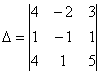 
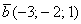
, в правую часть записаны координаты вектора 
.
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
, значит, система имеет единственное решение.
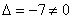
Дальнейшее – дело техники: 
Таким образом:
– разложение вектора по базису 
.
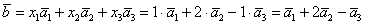
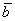
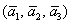
Ответ: 
Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы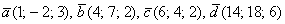 
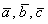
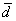
. Показать, что векторы 
образуют базис и найти координаты вектора 
в этом базисе. Систему линейных уравнений решить методом Крамера.
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
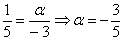
Ответ: при 
Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон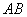 
и 
.
Найдём векторы:
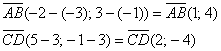
Вычислим определитель, составленный из координат векторов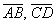 
:
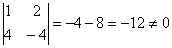
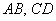
, значит, данные векторы не коллинеарны, и стороны 
не параллельны.
2) Проверим параллельность противоположных сторон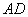 
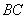
и 
.
Найдём векторы:
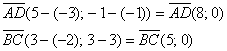
Вычислим определитель, составленный из координат векторов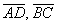 
:
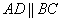
, значит, данные векторы коллинеарны, и 
.
Вывод: Две стороны четырёхугольника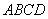 
параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
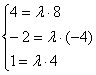
Система не имеет решения, значит, векторы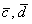 
не коллинеарны.
Более простое оформление:
– вторая и третья координаты не пропорциональны, значит, векторы не коллинеарны.
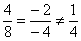
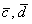
Ответ: векторы 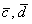не коллинеарны.
в) Исследуем на коллинеарность векторы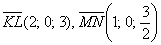 
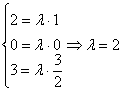
. Составим систему:
Соответствующие координаты векторов пропорциональны, значит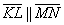 
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов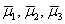 
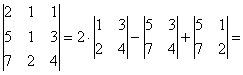
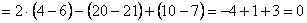
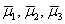
(определитель раскрыт по первой строке):
, значит, векторы линейно зависимы и не образуют базиса трёхмерного пространства.
Ответ: данные векторы не образуют базиса
Пример 9:Решение:Вычислим определитель, составленный из координат векторов :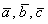
Таким образом, векторы 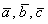линейно независимы и образуют базис.
Представим вектор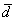 
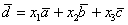
в виде линейной комбинации базисных векторов:
Покоординатно:
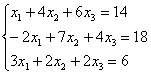
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
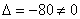
Ответ: Векторы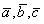 
образуют базис, 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Координаты вектора в пространстве и базис
Таким образом, справедлива следующая теорема.
Теорема 1.5 (о разложении вектора по базису в пространстве). Любой вектор может быть разложен по базису в пространстве, т.е. представлен в виде (1.4), где числа определяются однозначно.
1. Базис на прямой, на плоскости, в пространстве определяется неоднозначно. Например, если — базис в пространстве, то система векторов при любом также является базисом.
2. Следующие свойства выражают геометрический смысл линейной зависимости и линейной независимости векторов:
3. Понятие базиса непосредственно связано с понятием линейной независимости. Базис представляет собой упорядоченную совокупность линейно независимых векторов:
а) на прямой — это один линейно независимый вектор (см. пункт 1 замечаний 1.2);
б) на плоскости — это два линейно независимых вектора на этой плоскости, взятые в определённом порядке (см. пункт 2,»а»);
в) в пространстве — это три линейно независимых вектора, взятые в определённом порядке (см. пункт 2,»б»).
5. Теоремы 1.3-1.5 позволяют говорить, что базис — это максимальная линейно независимая система векторов (на прямой, на плоскости, в пространстве), так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
6. Базис — это полная линейно независимая система векторов (на прямой, на плоскости, в пространстве).
Ориентации базисов в пространстве
Базис в пространстве называется правым (или, что то же самое, упорядоченная тройка некомпланарных векторов называется правой тройкой), если, наблюдая из конца третьего вектора, кратчайший поворот от первого вектора ко второму виден происходящим против часовой стрелки (рис.1.33,а). Если описанный поворот виден происходящим по часовой стрелке, то базис называется левым (упорядоченная тройка некомпланарных векторов называется левой тройкой) (рис. 1.33,б).
Отметим следующие свойства: если тройка некомпланарных векторов — правая, то тройки, получающиеся «циклической» перестановкой трех векторов — также правые, а тройки, получающиеся перестановкой двух векторов или заменой одного вектора противоположным (например, — левые).
Векторное пространство: размерность и базис, разложение вектора по базису
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Таким образом, мы пришли к формулировке важнейшей теоремы:
Докажем эту теорему:
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Вектор x → будет представлен следующим образом:
Запишем это выражение в координатной форме:
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
Решение
Используем метод Гаусса:
Пусть в базисе вектор x → имеет координаты x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
Указанные системы являются также базисами заданного пространства.
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
В виде матрицы систему можно отобразить так:
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения: