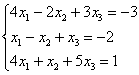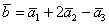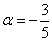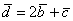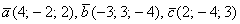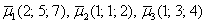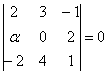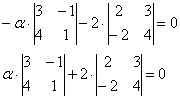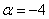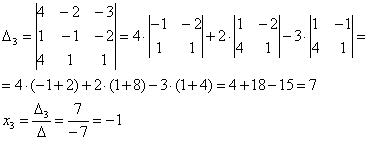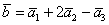Показать что система образует базис в пространстве
Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
Даны векторы 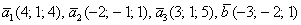

Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 

Вычислим определитель, составленный из координат векторов 
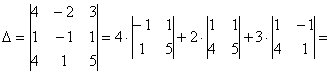
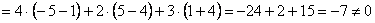

! Важно: координаты векторов 
Теперь вспомним теоретическую часть: если векторы 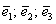
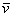
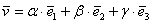
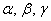
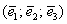
Поскольку наши векторы 
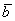
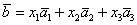
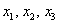
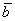
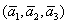
По условию и требуется найти координаты 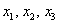
Для удобства объяснения поменяю части местами: 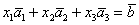
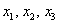
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 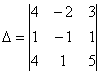
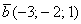
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
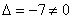
Дальнейшее – дело техники:
Таким образом:
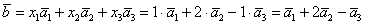
Ответ:
Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы 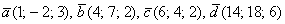
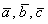
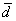
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
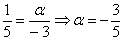
Ответ: при
Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон 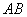
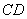
Найдём векторы:
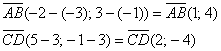
Вычислим определитель, составленный из координат векторов 
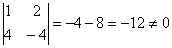
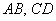
2) Проверим параллельность противоположных сторон 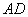
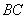
Найдём векторы:
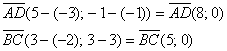
Вычислим определитель, составленный из координат векторов 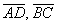

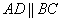
Вывод: Две стороны четырёхугольника 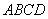
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
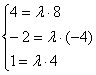
Система не имеет решения, значит, векторы 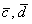
Более простое оформление:
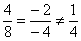
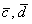
Ответ: векторы 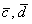
в) Исследуем на коллинеарность векторы 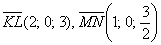
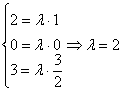
Соответствующие координаты векторов пропорциональны, значит 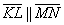
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов 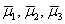
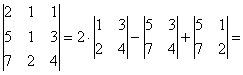
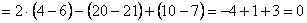
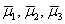
Ответ: данные векторы не образуют базиса
Пример 9:Решение:Вычислим определитель, составленный из координат векторов 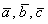

Таким образом, векторы 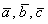
Представим вектор 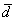
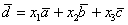
Покоординатно:
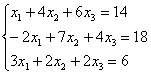
Систему решим по формулам Крамера:
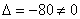
Ответ: Векторы 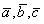
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
1.8.4. Базис и система координат пространства
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 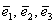
Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы 
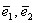
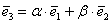
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга.
И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов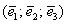
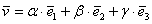
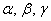
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов:
Выбранное (где угодно) начало координат 
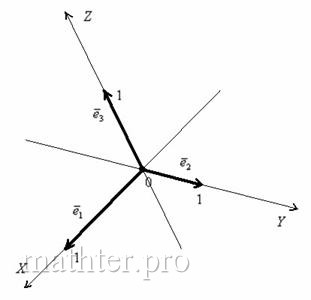
Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат 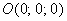
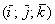
Ось абсцисс 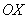
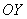
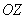
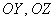
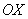
И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:
Для трёх векторов пространства эквиваленты следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры:
Три вектора пространства 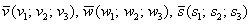
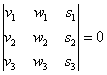
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Задача 42
Проверить, образуют ли векторы базис трёхмерного пространства:
а)
б)
а) Вычислим определитель, составленный из координат векторов 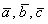

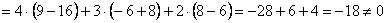
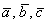
Ответ: данные векторы образуют базис.
б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор.
Решим творческую задачку:
Задача 43
При каком значении параметра 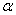
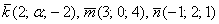
Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ: при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение 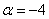
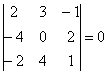
И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии:
Задача 44
Даны векторы 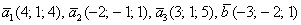
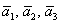
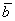
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 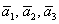
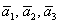
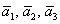
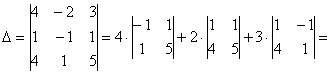
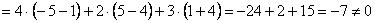
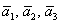
! Важно: координаты векторов 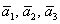
Теперь вспомним теоретическую часть: если векторы 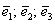
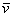
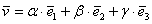
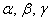
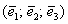
Поскольку наши векторы 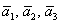
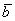
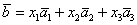
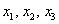
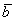
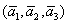
И по условию требуется найти координаты 
Для удобства объяснения поменяю части местами: 
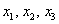
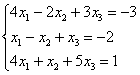
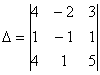
в правую часть записываем координаты вектора 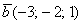
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден: 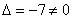
Дальнейшее дело техники: 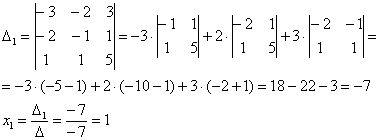
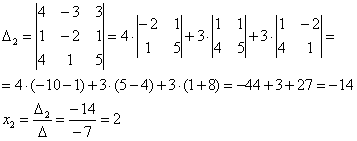
и ещё один определитель:
Таким образом:
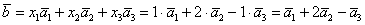
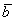
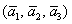
Ответ:
Такая же задача для самостоятельного решения:
Задача 45
Даны векторы 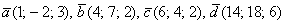
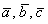
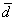
Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.