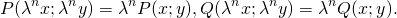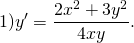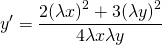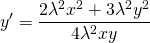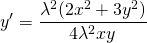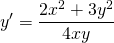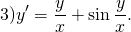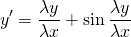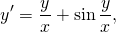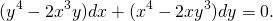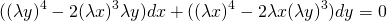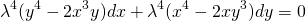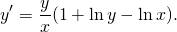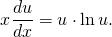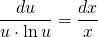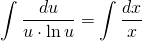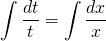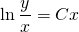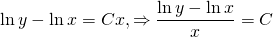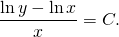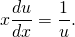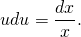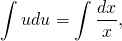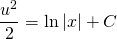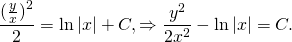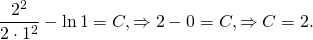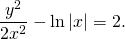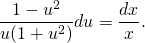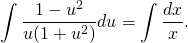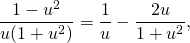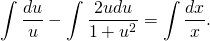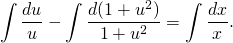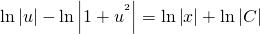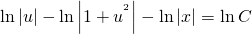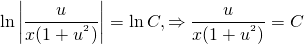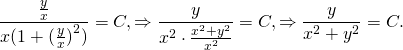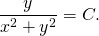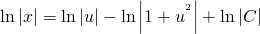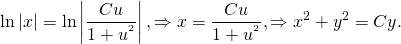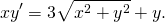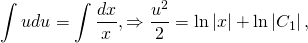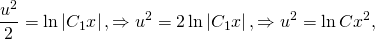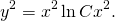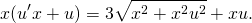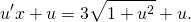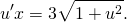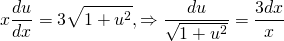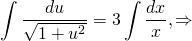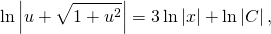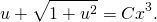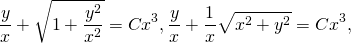Показать что данные дифференциальные уравнения являются однородными и решить их

Однородное дифференциальное уравнение можно решить с помощью подстановки $y = ux,$ которая преобразует однородное уравнение в уравнение с разделяющимися переменными.

Дифференциальное уравнение вида \[\left( <x + y + > \right)dx + \left( <x + y + > \right)dy = 0\] преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной: \[z = ax + by.\]

Нетрудно заметить, что многочлены $P\left( \right)$ и $Q\left( \right),$ соответственно, при $dx$ и $dy,$ являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным.

Интегрируем последнее выражение: \[\int = 2\int <\frac<>> \;\;\text<или>\;\;u = 2\ln \left| x \right| + C,\] где $C$ − постоянная интегрирования.

Возвращаясь к старой переменной $y,$ можно записать: \[y = ux = x\left( <2\ln \left| x \right| + C>\right).\] Таким образом, уравнение имеет два решения: \[y = x\left( <2\ln \left| x \right| + C>\right),\;\;x = 0.\]

Заметим, что корень $x = 0$ не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме: \[y’ = \frac\ln \frac = f\left( <\frac> \right).\] Как видно, уравнение является однородным.

Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде: \[ >><>> > = <\frac<<\frac<<>><<>>>><<\frac<><<>> + \frac<<>><<>>>> > = <\frac<<<<\left( <\frac> \right)>^2>>><<\frac + <<\left( <\frac> \right)>^2>>> > = > \right).> \] Сделаем подстановку $y = ux.$ Тогда $y’ = u’x + u.$ Подставляя $y$ и $y’$ в исходное уравнение, получаем: \[ <\left( > \right)\left( \right) = ,>\;\; <\Rightarrow u\left( \right)\left( \right) = .> \] Разделим обе части уравнения на $u.$ Заметим, что корень $x = 0$ не является решением, но можно убедиться, что корень $u = 0$ (или $y = 0$) будет одним из решений данного дифференциального уравнения.

Источник

Линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения 2-го порядка

Линейные однородные дифференциальные уравнения (ЛОДУ) и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка .

Частным случаем дифференциальных уравнений (ДУ) такого типа называют линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Общее решение линейного однородного дифференциального уравнения на отрезке [a;b] представляет собой линейную комбинацию 2х линейно независимых частных решений y₁ и y₂ нашего уравнения, т.е.:

Самое сложное заключается в определении линейно независимых частных решений ДУ такого типа. Зачастую, частные решения выбирают из таких систем линейно независимых функций:

Но достаточно редко частные решения представляются именно так.

Примером линейного однородного дифференциального уравнения можно назвать .

Общее решение линейного неоднородного дифференциального уравнения определяется как ,

где y₀ является общим решением соответствующего линейного однородного дифференциального уравнения,

а является частным решением исходного ДУ. Метод определения y₀ мы сейчас обсудили, а вычисляют, используя метод вариации произвольных постоянных.

Как пример линейного неоднородного дифференциального уравнения приводим .

Познакомиться ближе с теорией и просмотреть примеры решений можете здесь: Линейные дифференциальные уравнения второго порядка.

Источник

Как определить однородное уравнение

Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть

Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.

Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).

Подставляем вместо каждого x λx, вместо каждого y — λy:

Выносим лямбда в квадрате за скобки и сокращаем на него:

Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.

2) (x-y)ydx-x²dy=0.

Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:

(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).

Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:

После сокращения на λ получаем исходное уравнение:

а это значит, что данное уравнение является однородным.

Подставляем вместо каждого x λx, вместо каждого y — λy:

Делим обе части уравнения на лямбда в 4й степени:

Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).

Источник

Как решать дифференциальные уравнения

Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.

Основные понятия и определения

Определения

Типы уравнений

Алгоритм решения

ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.

Алгоритм нахождения общего решения:

После замены производной игрека исходное уравнение приобретает такой формат:

Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Однородные ДУ

Решается по следующему алгоритму:

Интегрируем обе части:

$$\lambda x \cdot \lambda y + (\lambda y)^2 = (2 (\lambda x)^2 + \lambda x\cdot \lambda y)y’$$

Ответ $$y^2 = Cxe^\frac<-y>$$

Линейные неоднородные ДУ

Алгоритм метода Бернулли:

Алгоритм метода вариации произвольной постоянной:

ДУ Бернулли

ДУ в полных дифференциалах

Ответ $$x^2+5xy+y^3 = C.$$

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:

Линейные однородные ДУ с постоянными коэффицентами

В зависимости от получившихся корней имеем общее решение в различных видах:

Ответ $$y = C_1 e^ <-2x>+ C_2 e^$$

Линейные неоднородные ДУ с постоянными коэффициентами

Ответ $$y = C_1 \cos x + C_2 \sin x + x\cos x + x^2\sin x$$

Метод Лагранжа

Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.

Источник

Как решить однородное дифференциальное уравнение

Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения: y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.

Примеры решения однородных дифференциальных уравнений 1-го порядка.

1) Решить уравнение

Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда

u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки

u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,

Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0

В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u

ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда

ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:

По свойству логарифмов:

Это — общий интеграл уравнения.

Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.

2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.

Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:

u’x=1/u. Так как u — функция от икса, u’=du/dx:

Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).

и поскольку в обеих частях стоят табличные интегралы, сразу же получаем

Выполняем обратную замену:

Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:

3) Найти общий интеграл однородного уравнения:

(x²-y²)dy-2xydx=0.

Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):

(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:

xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:

(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:

x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:

x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):

В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:

(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем: