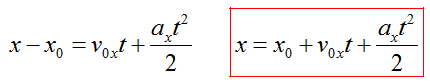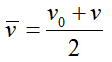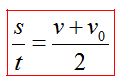Поезд разгоняется с ускорением а известно что к концу четвертой

Тест с ответами: “Равноускоренное движение”

1. Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 3 раза:
а) увеличится в 3 раза +
б) увеличится в 9 раз
в) уменьшится в 3 раза

2. Обычно движение с возрастающей по модулю скоростью называют:
а) ускоряемым движением
б) ускоренным движением +
в) равноускоренным движением

3. Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при увеличении скорости в 2 раза:
а) уменьшится в 2 раза
б) увеличится в 2 раза
в) увеличится в 4 раза +

4. Движение с убывающей скоростью:
а) замедленное движение +
б) заторможенное движение
в) тормозное движение

5. Поезд движется со скоростью 72 км/ч по закруглению дороги. Определите радиус дуги, если центростремительное ускорение поезда равно 0,5 м/с2:
а) 200 м
б) 360 м
в) 800 м +

6. При торможении направление ускорения … направлению скорости:
а) параллельно
б) противоположно +
в) зависит от условия задачи

7. Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна:
а) 12,5 м/с
б) 5 м/с
в) 10 м/с +

8. Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд таких чисел:
а) нечетных +
б) четных
в) зависит от условия задачи

9. Автомобиль на повороте движется по окружности радиусом 16 мс постоянной скоростью 36 км/ч. Каково центростремительное ускорение:
а) 4 м/с2
б) 1 м/с2
в) 6,25 м/с2 +

10. Два поезда идут навстречу друг другу: один – ускоренно на север, другой – замедленно на юг. Как направлены ускорения поездов:
а) одинаково на юг
б) одинаково на север +
в) один на север, другой на юг

11. Если вектор равнодействующей всех сил и вектор скорости направлены вдоль одной прямой, то тело движется прямолинейно, так ли это:
а) да +
б) нет
в) отчасти

12. Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6 м:
а) путь, пройденный поездом за четвертую секунду, больше 6 м
б) путь, пройденный поездом за четвертую секунду, меньше 6 м +
в) путь, пройденный поездом за четвертую секунду, равен 6 м

13. Если вектор равнодействующей всех сил и вектор скорости направлены вдоль пересекающихся прямых, то тело движется криволинейно, так ли это:
а) да +
б) нет
в) отчасти

14. Автомобиль прошел за первую секунду 1 м, за вторую секунду 2 м, за третью секунду 3 м, за четвертую секунду 4 м и т.д. Можно ли считать такое движение равноускоренным:
а) да
б) отчасти
в) нет +

15. Движение, при котором вектор ускорения не меняется по модулю и направлению:
а) равноускоренное движение +
б) равностороннее движение
в) равнозначное движение

16. Вагон наехал на тормозной башмак при скорости 4,5 км/ч. Через 3 с вагон остановился. Определите тормозной путь:
а) 10,8 м
б) 1,88 м +
в) 13,5 м

17. Пример равноускоренного движения:
а) парашютист, спускающийся на открытом парашюте
б) яблоко, падающее с дерева
в) велосипед, который катится с горки +

18. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2. На этом спуске его скорость увеличилась на 18 м/с. Велосипедист заканчивает свой спуск после его начала через:
а) 21,6 с
б) 15 с +
в) 7,5 с

19. Пример равноускоренного движения:
а) приземляющийся самолет
б) груша, падающая с дерева
в) камень брошенный под углом к горизонту +

20. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 0,5 м/с2. Сколько времени длится спуск:
а) 10 с
б) 20 с +
в) 5 с

21. Частным случаем равноускоренного движения является:
а) равнозамедленное движение
б) взаимозаменяемые движения
в) равноудаленное движение

23. Равноускоренное движение:
а) может происходить неограниченно долго
б) зависит от условий задачи
в) не может происходить неограниченно долго +

25. Движение по любой кривой, при котором составляющая ускорения, параллельная скорости, является постоянной:
а) косолинейное равноускоренное движение
б) линейное равноускоренное движение
в) криволинейное равноускоренное движение +

26. Какая физическая величина относится к векторным величинам:
а) путь
б) ускорение +
в) координата

27. Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется:
а) ускорением +
б) движением
в) увеличением

28. В каких единицах измеряется ускорение в СИ:
а) м/с
б) км/ч
в) м/с2 +

29. Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7 км/ч, во вторую – 9 км/ч, в третью 12 км/ч:
а) нет +
б) да
в) зависит от условий задачи

30. Равноускоренное движение является неравномерным движением, так ли это:
а) нет
б) да +
в) отчасти

Источник

Механика

Тестирование онлайн

Равноускоренное движение

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Ускорение тела

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».

Перемещение при равноускоренном движении

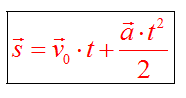
Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

Упражнения

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное

Источник

Поезд разгоняется с ускорением а известно что к концу четвертой

Нельзя, так как скорость движения воздушного шара равна скорости ветра.

В системе отсчета «Земля» точка колеса, соприкасающаяся с рельсом, имеет мгновенную скорость, равную нулю. В сторону, обратную движению вагона, перемещаются точки реборды, находящиеся ниже точки соприкосновения колеса и рельса.

Задача легко решается в системе координат, связанной с одной из машин. Пусть В неподвижна. Тогда машина А относительно В как бы участвует в двух движениях: со скоростью v₁ относительно земли и со скоростью вместе с землей. Построив параллелограмм (рис. 286), найдем скорость v₀ машины А относительно неподвижной машины В. Длина перпендикуляра ВС и выражает наименьшее расстояние, на которое сближаются машины.

Путь за какую-нибудь секунду любого движения численно равен средней скорости за эту секунду. Так как поезд движется с ускорением а>0, то скорость его все время возрастает. Если к концу четвертой секунды скорость равна 6 м/с, то в начале четвертой секунды она была меньше 6 м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6 м/с.

Источник

Движение с переменной скоростью

1.2.3 Поезд движется с ускорением а (а > 0). Известно, что к концу четвертой секунды скорость поезда равна 6 м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6 м?

1.2.4 На прямой дороге автомобиль ускоряется из состояния покоя до скорости 60 км/ч за 5 с. Какова величина его среднего ускорения?

1.2.9 С высоты 1000 м падает тело без начальной скорости. Одновременно с высоты 1100 м падает другое тело с некоторой начальной скоростью. Оба тела достигают Земли в один и тот же момент времени. Найти начальную скорость второго тела. Сопротивлением воздуха пренебречь.

1.2.11 За 10 с автомобиль равномерно ускоряется из состояния покоя до скорости 15 м/с, после чего в течение 10 с его скорость 15 м/c остается постоянной. Затем в последующие 5,0 с он равномерно тормозится до скорости 5 м/с. После чего его скорость сохраняется постоянной в течение 5 с. Постройте график зависимости а) скорости от времени, б) перемещения от времени.

1.2.12 Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющий одновременно двум условиям: а) средняя скорость за время от 2 до 6 с равна 5 м/с; б) максимальная скорость за это же время равна 15 м/с.

1.2.13 Две частицы в момент времени t = 0 вышли из одной точки. Определите по графикам зависимости скорости от времени место и время новой встречи частиц. Частицы движутся по одной прямой. (Рис. 8)

Рис.8	Рис.9
Рис. 10	Рис.11

1.2.14 Тело в течение времени t движется с постоянной скоростью v_0. Затем скорость его линейно нарастает со временем так, что в момент времени 2t она равна 2v₀. Определите путь, пройденный телом за время t > t.

1.2.15 Конькобежец проходит дистанцию L с постоянной скоростью, а затем тормозится с ускорением a. При какой скорости время движения до остановки наименьшее?

1.2.16 Из сферического аквариума радиуса R, наполовину заполненного водой, с каждой единицы поверхности испаряется в единицу времени объём жидкости q. Через какое время вся вода испарится?

1.2.17 По графику зависимости ускорения от времени установите скорость в моменты времени 4 и 15 с, если в момент времени 1 с скорость равна 3 м/с. (Рис. 9)

1.2.18 Оказалось, что график зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела v₀, время движения t₀. Определите путь, пройденный телом. (Рис. 10)

1.2.19 В коническом сосуде уровень воды поднимается с постоянной скоростью v. Как зависит от времени скорость поступления воды в сосуд через отверстие сечения s? В нулевой момент времени сосуд пуст. (Рис. 11)

1.2.20 Струя масла, попадающая на поверхность воды, растекается круговым пятном, которое имеет толщину h. Как зависит от времени скорость движения границы пятна, если в единицу времени поступает объём масла q? Начальный радиус пятна нулевой.

1.2.21 Тело начинает движение из точки A. Сначала тело движется в течение времени t равноускоренно, затем с тем же по модулю ускорением равнозамедленно. Через какое время от начала движения тело вернётся в точку A?

Дата добавления: 2015-09-15 ; просмотров: 19 ; Нарушение авторских прав

Источник

Поезд разгоняется с ускорением а известно что к концу четвертой

На рисунке приведён график зависимости модуля средней скорости V_р материальной точки от времени t при прямолинейном движении. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

3) За первые 3 с движения материальная точка проходит путь 8 м.

4) За первые 2 с движения материальная точка проходит путь 12 м.

5) Модуль начальной скорости материальной точки равен 2 м/с.

При равноускоренном движении средняя скорость равна полусумме начальной и конечной скорости. Найдем, чему равна скорость тела в момент времени t = 1 c:

Таким образом, ускорение тела равно

Путь — это произведение средней скорости на затраченное время

Обратите внимание, что на графике приведена зависимость средней скорости от времени, а не просто скорости. Наклон этого графика не равен ускорению.

Грузик массой m = 100 г неподвижно висит на лёгкой абсолютно упругой гибкой резинке с коэффициентом упругости k = 100 Н/м в поле силы тяжести с ускорением свободного падения g. Грузик поднимают из этого положения вертикально вверх на высоту h = 80 см, меньшую длины резинки, и отпускают без начальной скорости. Найдите время движения грузика вниз до точки его остановки. Начальной деформацией резинки при покоящемся грузике можно пренебречь.

Какие законы Вы используете для описания движения груза на резинке? Обоснуйте их применение к данному случаю.

Обоснование. Грузик движется поступательно, поэтому его можно принять за материальную точку. На первом этапе движения грузика на него действует только сила тяжести, т.к. сопротивлением воздуха мы пренебрегаем. Следовательно, на этом этапе грузик движется с ускорением свободного падения. И для описания движения тела можно применять законы прямолинейного равноускоренного движения.

На втором этапе движения резинка упруго деформируется, в результате чего на грузик начинает действовать изменяющаяся по модулю и направлению сила упругости, для которой справедлив закон Гука. Таким образом, второй этап движения представляет собой механические колебания груза на резинке. Т.к. сила тяжести не меняется по модулю и направлению, то она не влияет на характер колебаний грузика. В инерциальной системе отсчета возможно применение законов колебательного движения.

Перейдем к решению.

1. Введём неподвижную декартову систему координат с вертикальной осью ОХ, направленной вниз, причём начало координат поместим на уровне начального положения грузика.

2. После подъёма и отпускания грузика его движение вниз в поле силы тяжести разбивается на две стадии: вначале он свободно падает с ускорением g с высоты h до точки x = 0 (поскольку начальной деформацией резинки можно пренебречь) за время

что следует из формул кинематики равноускоренного движения.

3. Затем резинка начинает растягиваться, а грузик — тормозиться вплоть до остановки в нижней точке его движения. Поскольку начальное растяжение резинки компенсирует вес грузика, то на второй стадии можно считать, что действует только упругая сила, и уравнение движения (второй закон Ньютона) в проекции на ось ОХ имеет вид:

что является уравнением гармонических колебаний с периодом

4. С учётом начальных условий закон движения грузика на втором этапе представляет собой 1/4 часть периода синусоиды и происходит за время

5. Таким образом, искомое время движения грузика вниз до точки остановки равно

6. Подставляя численные данные из условия, получаем:

Ответ:

Источник