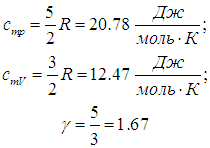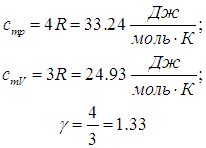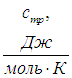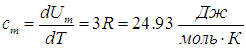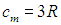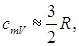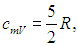Почему удельная теплоемкость при постоянном давлении больше чем удельная теплоемкость при постоянном
Краткая теория. Отношение удельной теплоемкости при постоянном давлении сp к удельной теплоемкости при постоянном объеме сv
Отношение удельной теплоемкости при постоянном давлении сp к удельной теплоемкости при постоянном объеме сv, называемое показателем адиабаты
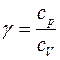
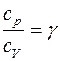
Адиабатным процессом называется процесс, осуществляющийся без теплообмена с внешней средой. Он протекает в системе, окруженной теплоизолирующей оболочкой, но его можно реализовать и при отсутствии такой оболочки. Для этого процесс должен протекать настолько быстро, чтобы за время его осуществления не произошло теплообмена между системой и окружающей средой. В настоящей лабораторной работе адиабатным можно считать быстропротекающий процесс расширения воздуха при открытом кране баллона.
В случае адиабатного процесса 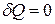
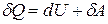
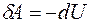
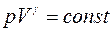

Выражение для γ в (2) следует из связи
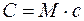
где М — молярная масса газа.
Удельной теплоемкостью с вещества называется физическая величина, численно равная количеству теплоты Q, необходимой для нагревания единицы массы вещества на один кельвин:
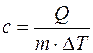

Молярной теплоемкостью С вещества называется физическая величина, численно равная количеству теплоты Q, необходимой для нагревания одного моля вещества на один кельвин:
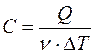

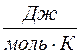
где ν – число молей вещества.
Для вещества в газообразном состоянии величина удельной и молярной теплоёмкостей газа существенно зависит от того, при каких условиях он нагревается: при постоянном объёме или при постоянном давлении. В первом случае сообщенное газу тепло идёт только на увеличение внутренней энергии газа, так как объём газа не изменяется и поэтому не совершается работа расширения. Во втором случае требуется дополнительное количество теплоты, необходимое для совершения работы расширения газа, так как неизменность давления обеспечивается увеличением объёма газа. Поэтому у газа различают две удельные и две молярные теплоёмкости: теплоёмкость при постоянном объёме и теплоемкость при постоянном давлении.
Учитывая, что для ν молей элементарное количество теплоты δQ = νCdT,
первое начало термодинамики 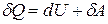
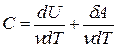
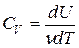
Здесь символ d употребляется для обозначения бесконечно малого приращения функции, а 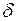
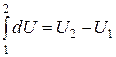
Элементарная работа 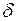
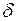
Молярная теплоемкость при постоянном давлении равна
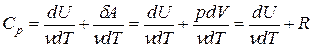
т.к. из уравнения Клапейрона-Менделеева PV = νRT следует, что 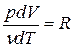
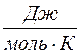
Таким образом, молярная теплоемкость Сp газа при постоянном давлении больше молярной теплоёмкости Cv при постоянном объёме на универсальную газовую постоянную R:
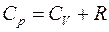
Это означает, что при изобарном процессе газу нужно сообщить кроме тепла, идущего на увеличение внутренней энергии, еще некоторое добавочное количество тепла, эквивалентное произведенной им внешней работе. Соотношение (8) называется уравнением Майера.
Известно, что внутренняя энергия ν молей газа определяется как U= 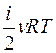
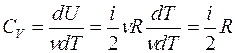
а с учетом уравнения Майера (8) молярная теплоемкость при постоянном давлении равна
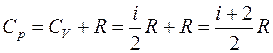
Для показателя адиабаты γ имеем
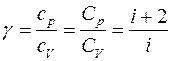
откуда видно, что величина g зависит только от числа степеней свободы молекул, из которых состоит газ.
Численное значение g различно для одно-, двух или многоатомных идеальных газов и зависит от числа i степеней свободы: для одноатомных i = 3, двухатомных
i = 5 и многоатомных i = 6.
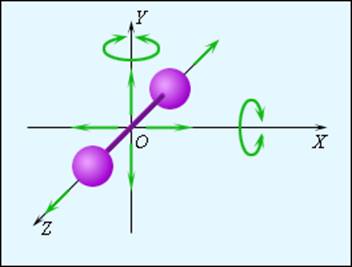
Число поступательных степеней свободы iпост равно 3 (в трехмерном пространстве поступательное движение центра масс молекулы можно описать тремя пространственными координатами х, у и z).
Процессы, при которых один из основных параметров состояния p, V, Т сохраняется постоянным, называются изопроцессами.
Изохорным называется процесс, протекающий при постоянном объеме V = =const, поэтому DV = dV = 0. Изохорный процесс описывается законом Гей-Люссака

Элементарная работа в изохорном процессе равна нулю: δA = pdV= 0, следовательно, все подводимое тепло идет на повышение внутренней энергии газа: δQ = δU.
Одним из методов определения показателя адиабаты γ для воздуха является метод Клемана и Дезорма, который также называют методом адиабатного расширения. Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединен-
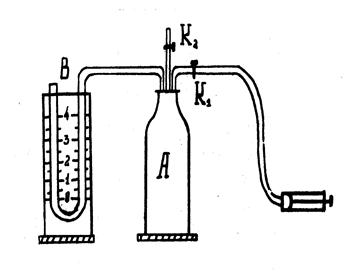 Рис. 1 Рис. 1 | Н | ного с водяным манометром В и насосом Н. Водяной U-образный манометр В измеряет избыточное, по сравнению с атмосферным, давление воздуха в баллоне А. Через кран К1 воздух нагнетается в баллон, а через кран К2 — выпускается. Если кран К2 открыт, баллон сообщается с атмосферным воздухом и давление р внутри него равно атмосферному, разность уровней воды в коленах манометра равна нулю, а температура Т в баллоне равна температуре окружающей среды. |
В процессе работы воздух, заключенный в баллоне, проходит последовательно три состояния.
1. Если закрыть кран К2 и накачать в баллон небольшое количество воздуха, то давление в баллоне станет выше атмосферного, что отмечается возникновением разности уровней воды в коленах манометра. При сжатии (накачке) воздух в баллоне нагревается выше комнатной температуры, после закрытия крана К2 начинается теплообмен с внешней средой через стенки баллона. Это процесс изохорного охлаждения, который прекращается, когда воздух в баллоне примет температуру окружающей среды T1. При этом разность уровней в манометре станет устойчивой и равной ρgh1, где ρ – плотность воды в манометре; g— ускорение свободного падения; h1 – разность уровней воды в коленах манометра. Состояние I воздуха в баллоне характеризуется температурой T1, давлением р1= р0+ ρgh1, где р0 – атмосферное давление, а ρgh1— добавочное давление, избыточное над атмосферным.
2. Если открыть и быстро закрыть кран К2, то часть воздуха выйдет из баллона и давление сравняется с атмосферным р0, а температура газа понизится до Т2
Теплоёмкость идеального газа
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
Во многих случаях удобно использовать молярную теплоемкость C:
где M – молярная масса вещества.
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе (p = const).
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
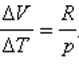 |
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
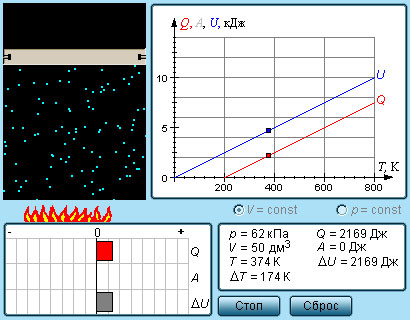
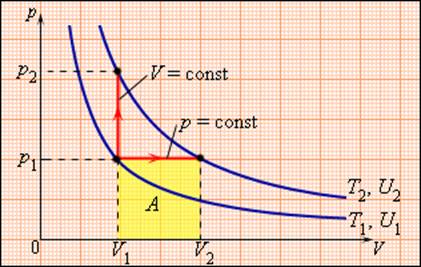
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости CV в процессе с постоянным объемом (рис. 3.10.1).
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
В частности, это отношение входит в формулу для адиабатического процесса.
Между двумя изотермами с температурами T1 и T2 на диаграмме (p, V) возможны различные пути перехода. Поскольку для всех таких переходов изменение температуры ΔT = T2 – T1 одинаково, следовательно, одинаково изменение ΔU внутренней энергии. Однако, совершенные при этом работы A и полученные в результате теплообмена количества теплоты Q окажутся различными для разных путей перехода. Отсюда следует, что у газа имеется бесчисленное количество теплоемкостей. Cp и CV – это лишь частные (и очень важные для теории газов) значения теплоемкостей.
 |
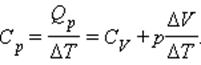
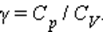
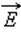 поступательного движения молекул и абсолютной температурой T:
поступательного движения молекул и абсолютной температурой T: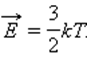
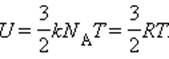
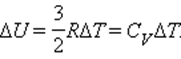
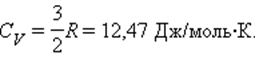
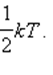
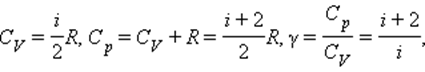
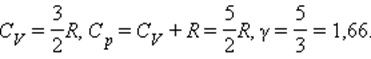
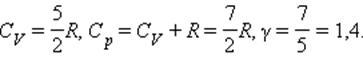
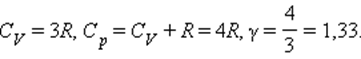
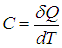
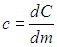
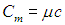
 ) на элементарное приращение абсолютной температуры dT, получим соотношение
) на элементарное приращение абсолютной температуры dT, получим соотношение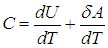
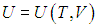 .
.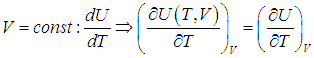 .
.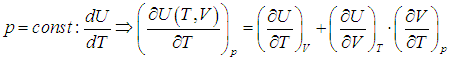
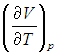 вычисляется с помощью уравнения состояния системы, записанного в виде
вычисляется с помощью уравнения состояния системы, записанного в виде 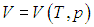 . Например, в частном случае идеального газа
. Например, в частном случае идеального газа ,
,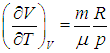 .
.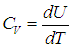
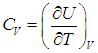

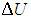 на
на 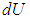 , а
, а 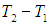 на
на 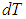 немедленно получаем:
немедленно получаем: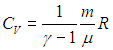 .
. ) следует выражение для элементарной работы при бесконечно малом изменении температуры
) следует выражение для элементарной работы при бесконечно малом изменении температуры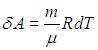
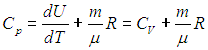
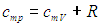
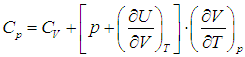
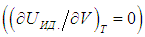 и использования его уравнения состояния (см. выше):
и использования его уравнения состояния (см. выше):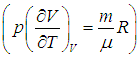 .
. ) для количества теплоты, получаемого идеальным газом при указанных процессах.
) для количества теплоты, получаемого идеальным газом при указанных процессах.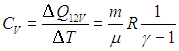
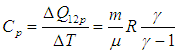

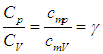
 ), а также ( 1.28
), а также ( 1.28 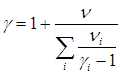 ) для смеси газов). Из формул ( 1.19
) для смеси газов). Из формул ( 1.19