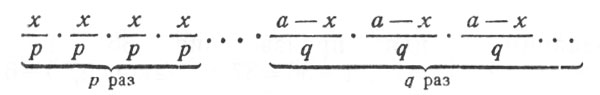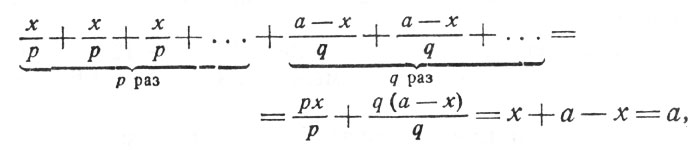Почему сумма всех чисел больше чем их произведение
math4school.ru
Когда произведение наибольшее?
Для решения многих задач «на максимум и минимум», т.е. на разыскание наибольшего и наименьшего значений переменной величины, можно успешно пользоваться некоторыми алгебраическими утверждениями, с которыми мы сейчас познакомимся.
Рассмотрим следующую задачу:
На какие две части надо разбить данное число, чтобы произведение их было наибольшим?
произведение двух чисел, сумма которых неизменна, будет наибольшим тогда, когда эти числа равны между собой.
x · y · z
Рассмотрим тот же вопрос для трех чисел.
На какие три части надо разбить данное число, чтобы произведение их было наибольшим?
При решении этой задачи будем опираться на предыдущую.
Пусть число а разбито на три части. Предположим сначала, что ни одна из частей не равна a /3 .Тогда среди них найдется часть, большая a /3 (все три не могут быть меньше a /3 ); обозначим ее через
Точно так же среди них найдется часть, меньшая a /3 ; обозначим ее через
Числа х и у положительны. Третья часть будет, очевидно, равна
Итак, если первые две части числа а заменить числами
а третью оставить без изменения, то произведение увеличится.
Пусть теперь одна из частей уже равна a /3 . Тогда две другие имеют вид
Если мы эти две последние части сделаем равными a /3 (отчего сумма их не изменится), то произведение снова увеличится и станет равным
Подобным же образом можно доказать эту теорему и для четырех множителей, для пяти и т.д.
x p · y q
Рассмотрим теперь более общий случай.
Надо найти, при каком значении х выражение
достигает наибольшей величины.
Умножим это выражение на число 1 /р p q q . Получим новое выражение
которое, очевидно, достигает наибольшей величины тогда же, когда и первоначальное.
Представим полученное сейчас выражение в виде
где множители первого вида повторяются p раз, а второго – q раз.
Сумма всех множителей этого выражения равна
т.е. величине постоянной.
На основании ранее доказанного заключаем, что произведение
достигает максимума при равенстве всех его отдельных множителей, т.е. когда
произведение х p y q при постоянстве суммы х + у достигает наибольшей величины тогда, когда
Таким же образом можно доказать, что
Источник: Я.И. Перельман. Занимательная алгебра (Москва, «Наука», 1970).
Что больше : сумма С всех чисел, меньших 100, или их произведение Р?
Что больше : сумма С всех чисел, меньших 100, или их произведение Р?
Больше сумма, так как произведение равно нулю.
Если все числа неотрицательные, конечно.
Может ли произведение двух чисел быть меньше их суммы?
Может ли произведение двух чисел быть меньше их суммы?
Покажите на примерах.
Что больше : сумма C всех чисел, меньше 100 или их произведение P?
Что больше : сумма C всех чисел, меньше 100 или их произведение P?
Обоснуй свой ответ.
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте?
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте.
Произведение суммы чисел 59 и 46 и меньше из этих чисел?
Произведение суммы чисел 59 и 46 и меньше из этих чисел.
Может ли произведение двух простых чисел быть простым числом?
Может ли произведение двух простых чисел быть простым числом?
Запиши : а) произведение суммы и разности этих чисел.
В) проиведение разности данных чисел и меньшего из них.
Г) произведение большего числа и часного этих чисел.
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте?
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте.
На сколько меньше сумма чисел 8 и 2, чем их произведение?
На сколько меньше сумма чисел 8 и 2, чем их произведение.
Может ли произведение двух простых чисел быть простым чеслом?
Может ли произведение двух простых чисел быть простым чеслом?
Произведение чисел 3806 и 1 меньше их суммы?
Произведение чисел 3806 и 1 меньше их суммы.
60 * 40 = 2400 120000 : 2400 = 50 ответ : 50.
НенавиделаЗмеяДобрынюза то, что не раз богатырьеёзмеёнышейядовитых топтал, не раз спасал от пленазмеиноголюдей русских, которыхЗмеясебе на гору в пещеру утаскивала.
404 : 4 = 101 409 : 4 = 102, 25 612 : 3 = 204 619 : 3 = 206, (3) 424 : 4 = 106 431 : 4 = 107, 75 По четвертому пункту не видно делителя.
7 / 35 = 24 / 120 35 / 7 = 120 / 24.
Ответ такой : 35 / 7 = 120 / 24 Проверяем : 35 : 7 = 5 120 : 24 = 5.
Делители 1, 2, 4, 7, 14, 28, 8669, 17338, 34676, 60683, 121366, 242732.
Почему сумма всех чисел больше чем их произведение
Когда произведение наибольшее?
Для решения многих задач «на максимум и минимум», т. е. на разыскание наибольшего и наименьшего значений переменной величины, можно успешно пользоваться одной алгебраической теоремой, с которой мы сейчас познакомимся. Рассмотрим следующую задачу:
На какие две части надо разбить данное число, чтобы произведение их было наибольшим?
Пусть данное число а. Тогда части, на которые разбито число а, можно обозначить через
число х показывает, на какую величину эти части отличаются от половины числа а. Произведение обеих частей равно
Ясно, что произведение взятых частей будет увеличиваться при уменьшении х, т. е. при уменьшении разности между этими частями. Наибольшим произведение будет при x = 0, т. е. в случае, когда обе части равны a/2.
Итак, число надо разделить пополам: произведение двух чисел, сумма которых неизменна, будет наибольшим тогда, когда эти числа равны между собой.
Рассмотрим тот же вопрос для трех чисел.
На какие три части надо разбить данное число, чтобы произведение их было наибольшим?
При решении этой задачи будем опираться на предыдущую.
Пусть число а разбито на три части. Предположим сначала, что ни одна из частей не равна a/3.Тогда среди них найдется часть, большая a/3 (все три не могут быть меньше a/3); обозначим ее через
Точно так же среди них найдется часть, меньшая a/3; обозначим ее через
Числа х и у положительны. Третья часть будет, очевидно, равна
больше, чем произведение первых двух частей числа а.
Итак, если первые две части числа а заменить числами
а третью оставить без изменения, то произведение увеличится.
Пусть теперь одна из частей уже равна a/3. Тогда две другие имеют вид
Если мы эти две последние части сделаем равными a/3 (отчего сумма их не изменится), то произведение снова увеличится и станет равным
Итак, если число а разбито на 3 части, не равные между собой, то произведение этих частей меньше чем а 3 /27, т. е. чем произведение трех равных сомножителей, в сумме составляющих а.
Подобным же образом можно доказать эту теорему и для четырех множителей, для пяти и т. д.
Рассмотрим теперь более общий случай.
Найти, при каких значениях х и y выражение х p у q наибольшее, если х + y = а.
Надо найти, при каком значении х выражение
достигает наибольшей величины.
которое, очевидно, достигает наибольшей величины тогда же, когда и первоначальное.
Представим полученное сейчас выражение в виде
Сумма всех множителей этого выражения равна
т. е. величине постоянной.
На основании ранее доказанного заключаем, что произведение
достигает максимума при равенстве всех его отдельных множителей, т. е. когда
Итак, произведение х p y q при постоянстве суммы х + у достигает наибольшей величины тогда, когда
Таким же образом можно доказать, что произведения
при постоянстве сумм x + y + z, x + y + z + t и т. д. достигают наибольшей величины тогда, когда
Почему сумма всех чисел больше чем их произведение
Когда произведение наибольшее?
Для решения многих задач «на максимум и минимум», т. е. на разыскание наибольшего и наименьшего значений переменной величины, можно успешно пользоваться одной алгебраической теоремой, с которой мы сейчас познакомимся. Рассмотрим следующую задачу:
На какие две части надо разбить данное число, чтобы произведение их было наибольшим?
Пусть данное число а. Тогда части, на которые разбито число а, можно обозначить через
число х показывает, на какую величину эти части отличаются от половины числа а. Произведение обеих частей равно
Ясно, что произведение взятых частей будет увеличиваться при уменьшении х, т. е. при уменьшении разности между этими частями. Наибольшим произведение будет при x = 0, т. е. в случае, когда обе части равны a/2.
Итак, число надо разделить пополам: произведение двух чисел, сумма которых неизменна, будет наибольшим тогда, когда эти числа равны между собой.
Рассмотрим тот же вопрос для трех чисел.
На какие три части надо разбить данное число, чтобы произведение их было наибольшим?
При решении этой задачи будем опираться на предыдущую.
Пусть число а разбито на три части. Предположим сначала, что ни одна из частей не равна a/3.Тогда среди них найдется часть, большая a/3 (все три не могут быть меньше a/3); обозначим ее через
Точно так же среди них найдется часть, меньшая a/3; обозначим ее через
Числа х и у положительны. Третья часть будет, очевидно, равна
больше, чем произведение первых двух частей числа а.
Итак, если первые две части числа а заменить числами
а третью оставить без изменения, то произведение увеличится.
Пусть теперь одна из частей уже равна a/3. Тогда две другие имеют вид
Если мы эти две последние части сделаем равными a/3 (отчего сумма их не изменится), то произведение снова увеличится и станет равным
Итак, если число а разбито на 3 части, не равные между собой, то произведение этих частей меньше чем а 3 /27, т. е. чем произведение трех равных сомножителей, в сумме составляющих а.
Подобным же образом можно доказать эту теорему и для четырех множителей, для пяти и т. д.
Рассмотрим теперь более общий случай.
Найти, при каких значениях х и y выражение х p у q наибольшее, если х + y = а.
Надо найти, при каком значении х выражение
достигает наибольшей величины.
которое, очевидно, достигает наибольшей величины тогда же, когда и первоначальное.
Представим полученное сейчас выражение в виде
Сумма всех множителей этого выражения равна
т. е. величине постоянной.
На основании ранее доказанного заключаем, что произведение
достигает максимума при равенстве всех его отдельных множителей, т. е. когда
Итак, произведение х p y q при постоянстве суммы х + у достигает наибольшей величины тогда, когда
Таким же образом можно доказать, что произведения
при постоянстве сумм x + y + z, x + y + z + t и т. д. достигают наибольшей величины тогда, когда
Что больше : сумма С всех чисел, меньших 100, или их произведение Р?
Что больше : сумма С всех чисел, меньших 100, или их произведение Р?
Больше сумма, так как произведение равно нулю.
Если все числа неотрицательные, конечно.
Может ли произведение двух чисел быть меньше их суммы?
Может ли произведение двух чисел быть меньше их суммы?
Покажите на примерах.
Что больше : сумма C всех чисел, меньше 100 или их произведение P?
Что больше : сумма C всех чисел, меньше 100 или их произведение P?
Обоснуй свой ответ.
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте?
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте.
Произведение суммы чисел 59 и 46 и меньше из этих чисел?
Произведение суммы чисел 59 и 46 и меньше из этих чисел.
Может ли произведение двух простых чисел быть простым числом?
Может ли произведение двух простых чисел быть простым числом?
Запиши : а) произведение суммы и разности этих чисел.
В) проиведение разности данных чисел и меньшего из них.
Г) произведение большего числа и часного этих чисел.
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте?
Может ли произведение двух простых чисел быть простым числом Ответ обоснуйте.
На сколько меньше сумма чисел 8 и 2, чем их произведение?
На сколько меньше сумма чисел 8 и 2, чем их произведение.
Может ли произведение двух простых чисел быть простым чеслом?
Может ли произведение двух простых чисел быть простым чеслом?
Произведение чисел 3806 и 1 меньше их суммы?
Произведение чисел 3806 и 1 меньше их суммы.
60 * 40 = 2400 120000 : 2400 = 50 ответ : 50.
НенавиделаЗмеяДобрынюза то, что не раз богатырьеёзмеёнышейядовитых топтал, не раз спасал от пленазмеиноголюдей русских, которыхЗмеясебе на гору в пещеру утаскивала.
404 : 4 = 101 409 : 4 = 102, 25 612 : 3 = 204 619 : 3 = 206, (3) 424 : 4 = 106 431 : 4 = 107, 75 По четвертому пункту не видно делителя.
7 / 35 = 24 / 120 35 / 7 = 120 / 24.
Ответ такой : 35 / 7 = 120 / 24 Проверяем : 35 : 7 = 5 120 : 24 = 5.
Делители 1, 2, 4, 7, 14, 28, 8669, 17338, 34676, 60683, 121366, 242732.